
Cracking Playfair Ciphers
In 2020, the Zodiac 340 cipher was finally cracked after more than 50 years of trying by amateur code breakers. While the effort to crack it was extremely impressive, the cipher itself was ultimately disappointing. A homophonic substitution cipher with a minor gimmick of writing diagonally, the main factor that prevented it from being solved much earlier was the several errors the Zodiac killer made when encoding it.
Substitution ciphers, which operate at the level of a single character, are children’s toys, the kind of thing you might get a decoder ring for from the back of a magazine. Homophonic substitution ciphers, which are designed to prevent frequency analysis by using more than one cipher character to denote frequent letters, are barely more secure - Mary, Queen of Scots was executed in 1587 after just such a cipher was intercepted and cracked.
I want to tell you about an alternative cipher, which is much more secure than a substitution cipher, but still simple enough to encode and decode by hand quickly. This particular cipher was successfully used as a field cipher in WWI as it would take hours or days to crack by hand.
And then, of course, we’re going to crack it.
There’s no practical purpose to this; I wanted to play around with code breaking techniques, and modern ciphers are too secure to be anything but discouraging, while substitution ciphers don’t present much of a challenge. I found this to be a rewarding exercise and recommend it to anyone who wants to play around with hobby-level cryptography.
The Playfair Cipher
The cipher in question is called the Playfair cipher. In accordance with Stigler’s law of eponymy, it was invented by Charles Wheatstone in 1854. (Playfair merely popularized it.) Lest you think Wheatstone was cheated out of credit, rest assured that he received due credit for the Wheatstone bridge, which was invented by Samuel Hunter Christie.
The Playfair cipher is designed to be done on paper, so places a great deal of emphasis on ease of use over security. No addition module 256 here!
A Playfair key is a 5x5 grid of unique letters:

Because there are 26 letters but only 25 spaces, we need to merge two letters; by convention this is done by replacing J with I. Also, we will have to omit all punctuation and ignore case. One easy way to generate a key that you can easily remember is to use a unique phrase or sentence and write it into the grid from left to right and top to bottom, skipping any duplicate letters and filling up the rest of the grid with any omitted letters in alphabetical order.
The encryption operates on pairs of letters (which I will refer to as digraphs from now on.) Let’s say the first two letters of your message are “SP.” You find those two letters on the grid and imagine they form two corners of a rectangle, like so:
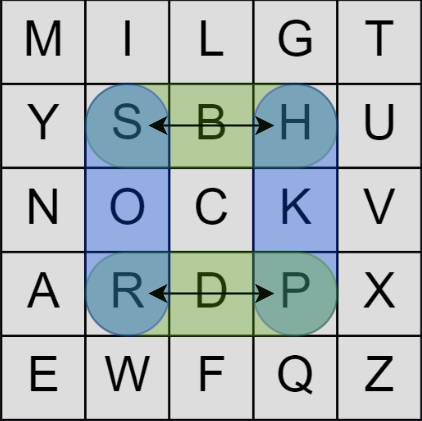
Then you simply swap each letter with the unused corner in the same row, resulting in “HR” which is our ciphertext. To decrypt ciphertext, you do the exact same operation.
That covers about 80% of the cases. However, there are a couple of other cases that can occur. If the letters are in the same row, instead of using the rectange corner swap, we simply shift each letter one space to the right, wrapping around to the leftmost column if we go off the right edge. If the letters are in the same column we shift each down one space, wrapping as needed. If the two letters are the same, we break them up by inserting a “Z” into the message: “LLAMA” becomes “LZLAMA” which becomes “TFMDYE”. If the duplicate letters happen to be “ZZ”, use X instead. And finally, if there are an odd number of letters in your message and you need one more letter to make a final digraph, stick a Z on the end (or X if the last letter was already a Z.)
These edge cases make the algorithm seem complicated but they rarely come up and 99% of the time you are just swapping corners or shifting by one within a row or column. It only takes five or ten minutes to learn the algorithm and once you do, and practice it a couple times on some moderately long messages, you’ll never forget it.
The reason it’s more secure that a substitution cipher is not merely because it operates two characters at a time, but because it mixes the two values together in a non-linear (but reversible) way. Modern block ciphers like AES use a substitution-permutation network which work in a very similar way and are difficult to crack for exactly the same reason.
We can visualize this strength using a heatmap. Here is the structure of a simple substitution cipher:
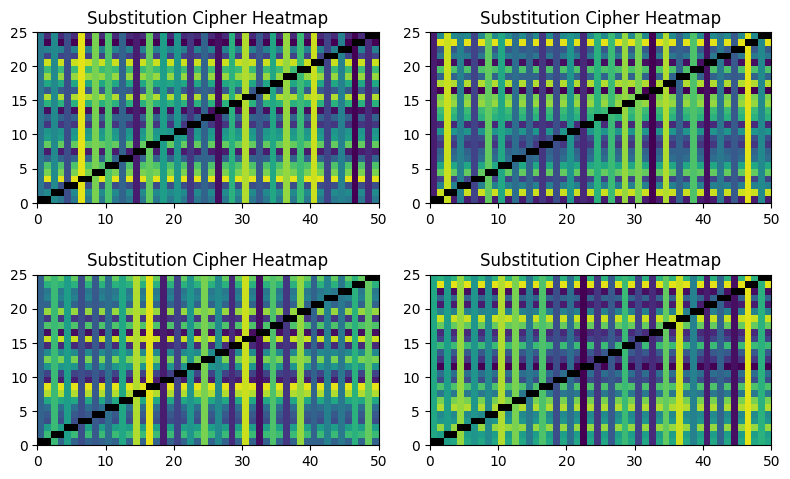
The patterns are obvious and simple; this cipher is not doing a good job of hiding the message. In contrast, the heatmap for the Playfair cipher shows reasonable levels of mixing:
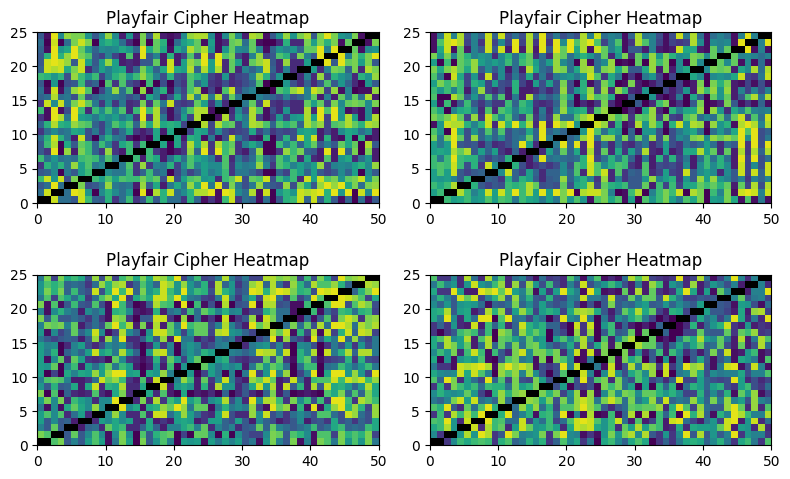
How secure is Playfair? Wikipedia has this to say:
Playfair is no longer used by military forces because of the advent of digital encryption devices. This cipher is now regarded as insecure for any purpose, because modern computers could easily break it within microseconds.
—Wikipedia
Really, microseconds? I’m not so sure about that… let’s be generous and say we can implement the Playfair decryption using 3 operations, and the bigraph lookup using 1 operation, all of which hit the L1 cache. That’s roughly 4 nanoseconds per bigraph, or 2 nanoseconds per character. We’ll need 100 characters or more to have any hope of cracking the cipher, so that’s 200 nanoseconds per candidate key that we check. That means we have to find a solution while checking fewer than 5,000 keys. That’s not much of a budget. I think the “milliseconds” used by Wikipedia is simply hyperbole, or perhaps a confusion between the cost of a decryption vs. the cost of a crack. To see why, let’s try to estimate the strength of a Playfair key from first principles.
At first glance is seems there should be $25! = 1.5 \times 10^{25}$ possible keys. However, if we study the algorithm, we see that all of the operations wrap around at the edges - that is, if the algorithm tells you to move one column to the right and you’re already at the 5th column, you wrap around back to the first column. The same is true for rows. That means Playfair keys can be visualized as being on a torus:

We can effectively rotate all the rows or columns of a key an obtain an equivalent key - they both perform the same encryption and decryption. This means there there are effectively only $25!/25 = 24! = 6.2 \times 10^{23}$ possible keys.
There are, broadly speaking, two ways to attack ciphers. The first is to search the space of all possible keys, decrypting the ciphertext with each candidate key and hunting for some kind of leaked information that might betray the fact that we’re getting closer. The second is obtain, by spycraft or guesswork, some plaintext message for which we also have the corresponding encrypted ciphertext (although the key is still unknown) and to mathematically deduce the key. We’ll do both, but let’s start with the second approach first, as it’s more fun - more like solving a puzzle and less like groping around in the dark.
Known Plaintext Attack
Known plaintext attacks sound rather pointless at first glance. “You’re telling me you can crack this cipher for me, but only if I give you the original message? I think I’ll take my business to a different cryptographer.”
It rather involved being on the other side of this airtight hatchway.
—Raymond Chen, quoting Douglas Adams
However, there are several ways to obtain probable plaintext. For example, you might guess it says “Keine besonderen Ereignisse,” German for “Nothing to Report,” a stock phrase often used by Germans in WWII and which was used to crack the Enigma machine. Nor is the exercise pointless - once you’ve cracked the cipher and obtained the secret key you’ll be able to use that key to decrypt and read other messages that you don’t yet know, as well as encrypt fake messages.
Stack Overflow user Ilmari Karonen has helpfully summarized the logic here. Some of the tricks are obvious, but others, like the chains which allow us to fill in an entire row or column, including the exact order, are extremely clever.
We have options about how we represent this problem to Z3. I found the most natural way was to use a 25x2 matrix, where each row represents a letter. The first column is the x-coordinate of that letter in the 5x5 playfair key grid, and the second is the y-coordinate. So every element of the matrix will be an integer between 0 and 4, and we’ll also need to make sure that a letter can go in one and only one cell. Because the constraints apply to all Playfair key grids, we’ll call them the universal constraints.
from z3 import *
X = [[Int('x_%i_%i' % (i, j)) for j in range(2)] for i in range(25)]
position_constraints = [
And(0 <= X[i][j], X[i][j] <= 4)
for j in range(2)
for i in range(25)
]
distinct_constraints = [
Distinct([X[i][0]*5 + X[i][1]
for i in range(25)])
]
universal_constraints = position_constraints + distinct_constraints
We’ll write some helper function so help keep track of the constraints. Most of the information will come in the form of learning that two letters are in the same row/column, or in adjacent rows/columns, so we’ll make it easy to describe such constraints.
def row_col_constraint(*indices, spacing=0, orientation=0):
constraints = [
(X[indices[i]][orientation] + spacing) % 5 == X[indices[i+1]][orientation]
for i in range(len(indices) - 1)
]
if len(constraints) >= 2:
return And(*constraints)
else:
return constraints[0]
def same_row(*indices):
return row_col_constraint(*indices, spacing=0, orientation=0)
def same_col(*indices):
return row_col_constraint(*indices, spacing=0, orientation=1)
def next_row(*indices):
return row_col_constraint(*indices, spacing=1, orientation=0)
def next_col(*indices):
return row_col_constraint(*indices, spacing=1, orientation=1)
Now we have to consider the various special cases. For example, if we see that the plaintext “XY” maps to ciphertext “AB”, and we also see that “AB” maps to “XY”, then we know that X, Y, A, B must form a rectangle in the key grid.

This gives us information about which letters must share a row or column, and we can encode this information as Z3 constraints:
# XY -> AB and AB -> XY, so XA/BY form a rectangle
def rectangle_constraint(plain_digraph: str, cipher_digraph: str) -> list:
p1, p2 = (playfair_ord(c) for c in plain_digraph)
c1, c2 = (playfair_ord(c) for c in cipher_digraph)
return And(
same_row(p1, c1),
same_row(p2, c2),
same_col(p1, c2),
same_col(p2, c1),
Not(same_row(p1, p2)),
Not(same_col(p1, p2)),
Not(same_row(c1, c2)),
Not(same_col(c1, c2))
)
There are several other such special cases to consider. Such as this chain constraints three in a row, either in a column or row:

In code:
# XY -> PQ, PQ -> YA => row/col of XPYQA
def chain_constraint(plain_digraph: str, cipher_digraph: str, next_digraph) -> list:
p1, p2 = (playfair_ord(c) for c in plain_digraph)
c1, c2 = (playfair_ord(c) for c in cipher_digraph)
n1, n2 = (playfair_ord(c) for c in next_digraph)
return Or(
And(same_row(p1, c1, p2, c2, n2), next_col(p1, c1, p2, c2, n2)),
And(same_col(p1, c1, p2, c2, n2), next_row(p1, c1, p2, c2, n2))
)
# XY -> PQ, PQ -> BX => row/col of YQXPB
# omitted for brevity...
# XY -> YZ so XYZ share a row or column and are all adjacent
def adjacent_constraint(plain_digraph: str, cipher_digraph: str) -> list:
p1, p2 = (playfair_ord(c) for c in plain_digraph)
c1, c2 = (playfair_ord(c) for c in cipher_digraph)
assert p2 == c1
return Or(
And(same_row(p1, p2, c2), next_col(p1, p2, c2)),
And(same_col(p1, p2, c2), next_row(p1, p2, c2))
)
# XY -> WX so YXW share a row or column and are all adjacent
# omitted for brevity...
However, even if we don’t see any special pattern, we do actually glean a small amount of information from every digraph we see. Remember, there are only three cases for encoding a pair: the rectangle case, the same row case, and the same column case. In all three, the ciphertext letter is always in the same row or the same column as the plaintext letter. If it’s the same column, then the ciphertext letter is immediately below the plaintext character:

This is true for both the first and second character of each digraph. In code:
# XY -> AB (no other information)
def simple_constraint(plain_digraph: str, cipher_digraph: str) -> list:
p1, p2 = (playfair_ord(c) for c in plain_digraph)
c1, c2 = (playfair_ord(c) for c in cipher_digraph)
return And(
Or(same_row(p1, c1), And(same_col(p1, c1), next_row(p1, c1))),
Or(same_row(p2, c2), And(same_col(p2, c2), next_row(p2, c2)))
)
It’s easy to scan through the known text and quickly build up a map of digraphs. This is also a good opportunity to validate that the ciphertext really does look like it came from Playfair cipher.
def parse_bigraph_map(plaintext: str, ciphertext: str) -> dict:
"""
Parse and validate matching plaintext and ciphertext. A dict of distinct
plaintext to ciphertext bigraphs mappings are returned, including all
mirrored mappings. This checks for obvious violations of the Playfair
cipher algorithm and will raise an Exception if any are found.
"""
# we only care about unique/distinct digraph mappings of the form AB -> XY
# and will ignore duplicates.
bigraph_map = {}
for plain_bigraph, cipher_bigraph in zip(bigraphs(plaintext), bigraphs(ciphertext)):
# XY -> AB => YX -> BA, add both the original and mirrored versions to the map
bigraph_map[plain_bigraph] = cipher_bigraph
bigraph_map[ plain_bigraph[::-1] ] = cipher_bigraph[::-1]
return bigraph_map
We have to examine each digraph mapping to see if we have enough information to identify a special case:
def constraints_from_known_text(plaintext: str, ciphertext: str, verbose_level=0) -> list:
"""
Analyze the plain/ciphertext bigraph pairs of a message and make deductions about
the structure of the key. These are returns as a list of Z3 constraints.
"""
bigraph_map = parse_bigraph_map(plaintext, ciphertext)
# build up constraints
constraints = []
seen_already = set()
for plain_bigraph, cipher_bigraph in bigraph_map.items():
# we only need to handle one of each mirror version.
if plain_bigraph[::-1] in seen_already:
continue
else:
seen_already.add(plain_bigraph)
# XY -> YZ => XYZ in row or col
if plain_bigraph[1] == cipher_bigraph[0]:
constraints.append( adjacent_constraint(plain_bigraph, cipher_bigraph) )
continue
# XY -> ZX => YXZ in row or col
# omitted for brevity
if cipher_bigraph in bigraph_map:
next_bigraph = bigraph_map[cipher_bigraph]
# XY -> AB, AB -> XY => rectangle
if next_bigraph == plain_bigraph:
constraints.append( rectangle_constraint(plain_bigraph, cipher_bigraph) )
continue
# XY -> PQ, PQ -> YA => row or col of XPYQA
if plain_bigraph[1] == next_bigraph[0]:
constraints.append(
chain_constraint(plain_bigraph, cipher_bigraph, next_bigraph))
continue
# XY -> PQ, PQ -> BX => rol or col of YQXPB
# omitted for brevity
# AB -> XY
constraints.append( simple_constraint(plain_bigraph, cipher_bigraph) )
return constraints
Now that we’ve built up a set of Z3 constraints describing our specific problem, we can ask Z3 to find a key meeting all of the above constraints:
def solve_playfair_constraints(dynamic_constraints):
solver = Solver()
solver.add(universal_constraints)
solver.add(dynamic_constraints)
# Check for solution
check = solver.check()
if check == sat:
model = solver.model()
grid = model_to_grid(model)
return sat, grid
else:
return check, None
We can also get Z3 to keep generating different unique solutions through the simple trick of adding a constraint to block the previous solution and re-solving:
def iter_playfair_constraints(dynamic_constraints):
solver = Solver()
solver.add(universal_constraints)
solver.add(dynamic_constraints)
# Check for solution
while True:
check = solver.check()
if check == sat:
model = solver.model()
grid = model_to_grid(model)
yield grid
# block the found solution and try again
solver.add(Or([
X[i][j] != model[X[i][j]]
for i in range(25)
for j in range(2)
]))
else:
break
When given only the first 100 characters as known plaintext, this approach was able to recover almost the entire key, except for a transposition of Z and X in the last row.
M Y N A E
I S O R W
L B C D F
G H K P Q
T U V Z X
This is enough to recover most of the message:

I was very impressed with Z3’s capabilities for this task. It was quite easy to express the constraints in its DSL and its performance was really good. The exact time it takes to find a key depends on how many characters of known plaintext we are able to provide; it usually requires about 100 to identify the correct key (or at least one close enough to work in practice) and that only takes a few seconds. However, that’s still three orders of magnitude out from the “microseconds” the Wikipedia article claimed, and tracking down known plaintext is kind of a pain, so let’s try another approach.
Guessing Plaintext
As the Wikipedia article points out, one way of acquiring probable plaintext sequences from Playfair ciphertext is to make educated guesses at known plaintext from patterns in the ciphertext.
First, and most obviously, Playfair always encrypts a given digraph to the same ciphertext everywhere in the message. So if we see ciphertext of the form “XY????XY”, where the digraph XY shows up twice with an even number of letters between them, then we know that the plaintext has some other digraph, say AB, with the same number of letters between them: “AB????AB”. Of course, we don’t know that it’s AB per se; it could be RE or CH. All we know is that there is a repetition in the plaintext as well.
Second, and only slightly less obviously, digraph encryption is symmetrical: if Playfair encrypts a digraph “AB” as “XY”, then it must also encrypt “BA” as “YX”. Therefore, if we see ciphertext with the pattern “XY????XY”, then we know the plaintext follows the pattern “AB????BA”.
The reason this is useful is because there are a limited number of words in the English language that match these patterns. For example, here is a list set of common English words having a gap of two letters between such patterns:
BAseBAll
CHurCH
DEciDE
EDitED
PErsPEctive
POstPOsted
REtiREment
Let’s say we see a pattern like “XY??XY”. If we guess that this matches “postposted” - that gives us 10 characters of known plain text to work with.
I wrote a program to identify all common English words containing such patterns:
import re
def has_digraph_pair(word: str, flipped=False):
if flipped:
pattern = r'(.)(.)(.*)\2\1'
else:
pattern = r'(.)(.)(.*)\1\2'
match = re.match(pattern, word)
if match:
return (match.group(1) + match.group(2)), len(match.group(3))
else:
return '', 0
digraph_pair_index = {}
with open('count_1w.txt', 'r') as file:
for index, line in enumerate(file.readlines()):
word, freq = line.split()
for flipped in (True, False):
digraph, gap = has_digraph_pair(word, flipped)
if digraph:
key = (flipped, gap)
candidates = digraph_pair_index.get(key, [])
candidates.append( (word, digraph, index, int(freq)) )
digraph_pair_index[key] = candidates
The program identified 161 words in all, but for any given pattern (gap length & flipped or not) there are usually only about a dozen words to try. I estimate the prevalence of such patterns is about one matching pattern for every 75 characters of ciphertext, so if you have 1,000 characters of ciphertext, you might expect to find 13 matching patterns, each of which given you a dozen or so words to try that might or might not yield about 10 characters of known plaintext.
The problem, as I see it, is that there is a combinatoric explosion of different combinations to try. For the pattern XYXY you might guess “immigration”, for a separate pattern WZ????ZW you might try “students”, for UV??????VU you might try “researchers”, and so on. But you’d have to try every possible combination and run the KPA attack for each one. It’s possible but it doesn’t feel like the most efficient approach, so even though I think this approach is very clever, I decided to give up on it and not take it any further.
A Sense of Rightness
More importantly, how do we know if we’re getting close? Detecting correct English is pretty easy; how do we detect partially decrypted, garbled English and distinguish it from pure gibberish?
The FBI, in a report on Graysmith’s 1979 attempt to crack the Zodiac 340 cipher, made this rather damning statement:
When a cryptogram has been decrypted properly there is an unmistakable sense of rightness about the solution. This sense of rightness is completely absent in the proposed solution.
— FBI
If we are to automate the search, we need to quantify this “sense of rightness.”
The traditional approach is to use trigrams or quadgrams and compare frequencies against the known frequencies of a target language such as English. For example, the trigram “THE” is very common in English, while “QXZ” is very uncommon, so if we see “THE” in the recovered plaintext we can know we are on the right track.
An out-of-the-box approach might work to a certain degree, but is far from optimal. To do a better job, we need to think carefully about the specifics of the Playfair algorithm.
First, the pre-processing steps of replacing “J” with “I” and breaking up pairs like “LL” by inserting an “X” to get “LX” mess up the frequencies a bit. If we’re going to use n-grams, we should recalculate frequency based on already pre-processed text. Second, Playfair works on pairs of letters. Especially very early in the search process, it’s a promising signal if any pair of letters decodes to a common English bigram. However, bigrams are a fairly weak way of detecting correct text. The code for this is fairly pedestrian so is omitted here, but you can read the source code if you like.
As an aside, I tried using ChatGPT (via the OpenAI API) to detect English. This works but is very slow - multiple seconds to check one message, when we need to be trying thousands or even millions of keys. However, it does work really well; ChatGPT can segment and punctuate text that’s been run together, and even tell if a message is messy/malformed English or complete gibberish. This is actually quite impressive because word segmentation is a classic example of a problem that needs something like dynamic programming to do efficiently, but ChatGPT can somehow do it with a single forward pass through the text.
@retry(stop=stop_after_attempt(3), wait=wait_exponential(multiplier=1, min=4, max=10))
def punctuate(text: str) -> Tuple[str, str]:
"""
Calls the OpenAI API to punctuate and format the input text, then extracts the
formatted text from the API response.
Args:
text (str): The input text to punctuate and format.
Returns:
Tuple[str, str]: The formatted text and any additional text returned by the API.
"""
chat_response = openai.ChatCompletion.create(
model="gpt-3.5-turbo",
messages=[
{"role": "system", "content": "As an AI with advanced language
understanding, your task is to punctuate and format the
following unpunctuated and unformatted text. Insert whitespace
and appropriate punctuation marks such as periods, commas,
exclamation points, and question marks. Do not change letters,
except to change case from uppercase to lowercase or to swap
the letters 'I' and 'J'. Only alter whitespace and punctuation;
do not attempt to fix grammar or misspellings. Break the text
into separate sentences and paragraphs to make it more
readable. Wrap lines at approximately 120 characters. Surround
the returned content with triple single quotes '''like this'''
and place any other comments outside of those triple quotes."},
{"role": "user", "content": ""},
{"role": "user", "content": "NEXTASTHEMOONSGENTLEEMBRACE
NURTURESTHENIGHTTHELIONPROWLSINREGALSPLENDOR"}, {"role":
"assistant", "content": "'''Next, as the moon's gentle embrace
nurtures the night, the lion prowls in regal splendor.'''"},
{"role": "user", "content": text}
],
temperature=0.0 # deterministic
)
response_text = chat_response['choices'][0]['message']['content']
formatted_text = extract_text(response_text)
if formatted_text:
other_text = response_text.replace("'''" + formatted_text + "'''", "")
return formatted_text, other_text
else:
return "", response_text
Unfortunately, we need to check thousands of texts per second during the course of a single crack, and ChatGPT is both far too slow and far too expensive to do that. Therefore the ChatGPT approach was dropped in favor of more heuristic but much more performant algorithms.
I found a good compromise was to apply word segmentation, and then to check the resulting words against an English dictionary, with partial credit for typos or misspellings (which may be decryption errors, or intentional mistakes designed to make the message harder to crack.) For this purpose we use an off-the-shelf Python package for word segmentation, implemented a BK-tree to find English words and near words, and wrote a heuristic function to gauge the “Englishness” of a text:
def english_word_score(word: str) -> int:
"""
Score the given word based on its presence in English language and its
edit distance from English words.
The scoring strategy is as follows:
1. If the word is in the set of English words, it's given a score equal
to its length.
2. If the word is not in the English words set but is within an edit
distance of 1 (according to the Damerau-Levenshtein distance) from a
word in the set, its score is two-thirds of its length.
3. If the closest edit distance is 2, its score is one third its
length.
4. Otherwise, its score is 0.
Args:
word (str): The word to score.
Only alphabetic characters are considered. Case is ignored.
Returns:
int: Score of the word.
"""
# Only consider alphabetic characters and ignore case
word = re.sub(r'[^a-z]', '', word.lower())
if word in english_words_lower_alpha_set:
return len(word)
elif len(word) > 2 and english_bk_tree.search(word, n=1, max_results=1):
return len(word) * 2/3
elif len(word) > 3 and english_bk_tree.search(word, n=2, max_results=1):
return len(word) * 1/3
else:
return 0
def percent_english(segmented_text: str, power=1.5):
"""
Returns the approximate percentage of the text which is comprised of
full english words.
Args:
text (str) : The segmented text. If not already clean and
segmented, use `scrub()` and `segment()` first.
power (float): Defaults 1.5. Raises each word score to this power,
giving more weight to longer words. We recommend a power between
1.0 and 2.0.
Returns:
float: Percentage between 0 and 1.
"""
# Segment the text
segmented_words = segmented_text.split(" ")
# Sum the lengths of English words
english_char_count = sum(english_word_score(word)**power for word in segmented_words)
# Total character count (excluding spaces)
total_char_count = sum(len(word)**power for word in segmented_words)
# Calculate the percentage
percentage = (english_char_count / total_char_count)
return percentage
This approach is still a little slow (still less than a second) but seemingly quite reliable. Nonsense gets scores under 10%, while even very bad/malformed English usually gets over 80%. It’s not fast enough to use for inner loop of the search, but it is fast and reliable enough to automatically detect when we’ve truly cracked the cipher, and so can be used as a final check to decide when to stop. (This is surprisingly difficult!)
To summarize, we automate the “sense of rightness” using a threefold approach:
- Use bigrams, but only on pairs of letters decoded together. This helps early on.
- Also use trigrams, to help zero in on the final key once it starts to make sense.
- Finally, use a slower method to verify that we’ve found a real English sentence.
Using these scoring techniques, we can do a good enough job identifying English text to tell if we are making progress on the crack or not. The next step is to use this information to guide us towards the correct solution.
Simulated Annealing
Before we talk about the Playfair crack itself, let’s discuss optimization in more general terms. There are a ton of optimization algorithms, but many of them require the objective function to be of a special form (linear or quadratic, say) or require you to have access to the first or even second order derivative. If all you have is some opaque, non-linear, non-convex function without a known gradient, you’re in the realm of derivative-free optimization.
We also have the problem that our input is a discrete string, not a continuous space, which further rules out many of the options. Of the remaining algorithms, I chose simulated annealing as being a good fit.
Simulated annealing is actually quite an interesting and powerful technique. Consider this function:
\[ f(x) = \sum_{k=1}^{1000} \frac{{|\sin(k\pi x)|}}{k} \]
Or in Python:
def f(x, n=1000):
return sum( abs(sin(k*pi*x))/k for k in range(1, n+1) )
This function has 84,779 local minima between 0.2 and 0.8:
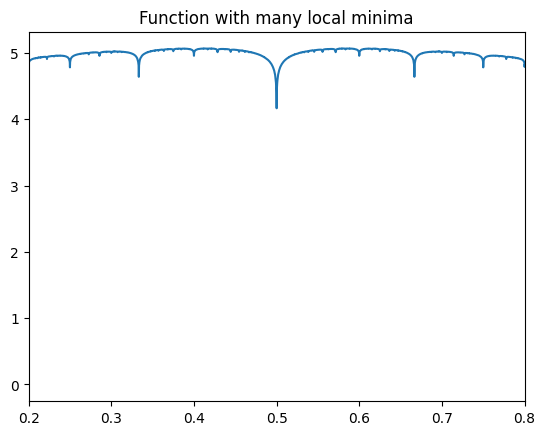
Now, I know that as a human, you can easily see that the true global minima is at 0.5, and a mathematician could easily prove this from the form of the function above. But let’s pretend that this function is opaque and see how the optimization algorithms do without human insight. From that point of view, this is a pathological function that is known to confuse most gradient descent style algorithms.
However, let’s take a stab at it with simulated annealing, which we can easily do with scipy:
from scipy.optimize import dual_annealing
dual_annealing(f, [(0.2, 0.8)], x0=[0.20001], callback=print)
Output:
[0.5008241] [4.56639717] 0
[0.5] 4.089060034436875 1
message: ['Maximum number of iteration reached']
success: True
status: 0
fun: 4.089060034436875
x: [ 5.000e-01]
nit: 1000
nfev: 2145
njev: 72
nhev: 0
The final solution found is that x value of 0.5, which it found in a few milliseconds
starting from a random initial point. It’s very powerful!
Intuitively, the way the algorithm works is by starting from some initial point and evaluating the score function at that point. Then, it makes a change to that point and re-evaluates. If the score improved, great; we’ll keep the new point. If the score got worse, then we have a tougher judgment call to make. At the beginning of search, we don’t mind going downhill sometimes - we have to if we want to avoid getting stuck in local minima. Our priority at first is the explore the whole space. However, later on, once we’ve found a “pretty good” solution, we’ll want to build on that. We might be willing to accept a lateral move or even a slightly downward one, but late in the search we’ll want to avoid throwing away all our hard work.
Simulated annealing’s solution to the differing priorities early and late in the search is to introduce a “temperature” which measures our willingness to move downhill. We start at a high temperature and will often accept downward moves in order to explore the full space, but as the temperature decreases we’ll become more conservative and reject moves that seem like we’ll losing too much progress. (This, in some way that I don’t know enough metallurgy to fully understand, parallels the annealing process that occurs when a material is treated by being heated and cooled.)
When cracking Playfair ciphers, the space we’re exploring is the space of all possible keys, which are distinct permutations of the 25 letters of the alphabet (I and J are merged into one to fit the 5x5 grid.) This is a discrete space, but in many ways acts like high dimensional space. It’s easy to get lost in high dimensional spaces, and it’s possible to wander away from a “pretty good” key and not be able to find your way back. Therefore, we also implement a “restart patience” concept, where we forcibly reset to the best known solution if we’ve been wandering blindly for a while and seem to have lost our way.
def simulated_annealing_crack(
cipher_text: str,
CipherClass: type,
score_fn,
attempts: int = 1024,
temperature: float = 0.5,
cooling_rate: float = 0.003,
restart_patience=256,
verbose: bool = False,
starting_key: str = None,
delta_log: list = None
) -> tuple[str, float, float]:
"""
Performs simulated annealing cracking on a cipher text using the
specified CipherClass.
Args:
cipher_text (str): The encrypted text to crack.
CipherClass (type): The class representing the cipher.
score_fn (function): The scoring function used.
Passed candidate plain text. Higher is better.
attempts (int, optional): The number of attempts to make.
Defaults to 1024.
acceptance_rate (float, optional): The acceptance rate for worse
solutions. Defaults to 0.5.
cooling_rate (float, optional): The cooling rate for the acceptance
rate. Defaults to 0.003.
verbose (bool, optional): Whether to print progress information.
Defaults to False.
starting_key (str, optional): The initial key to start with. If
None, a random key will be generated. Defaults to None.
Returns:
tuple[str, float]: A tuple containing the best key, its score, and
the final temperature.
"""
if starting_key is None:
current_key = CipherClass.make_random_key()
else:
current_key = starting_key
current_score = score_fn(CipherClass(current_key).decrypt(cipher_text))
best_key = current_key
best_score = current_score
time_since_best = 0
try:
for index in range(attempts):
candidate_key = CipherClass.alter_key_randomly(current_key)
cipher = CipherClass(candidate_key)
plain_text = cipher.decrypt(cipher_text)
score = score_fn(plain_text)
delta = score - current_score
delta_ratio = delta / temperature
if abs(delta_ratio) > 100:
delta_ratio = math.copysign(100, delta)
acceptance_rate = math.exp(delta_ratio)
if delta_log is not None:
delta_log.append((index, score, delta, temperature, acceptance_rate))
if random.random() < acceptance_rate:
current_score = score
current_key = candidate_key
if score > best_score:
time_since_best = 0
best_score = score
best_key = current_key
if verbose:
timestamp = datetime.now().strftime("%H:%M:%S")
print(index, timestamp,
best_key, best_score, temperature, plain_text[:50])
else:
time_since_best += 1
if time_since_best > restart_patience:
time_since_best = 0
score = best_score
current_key = best_key
temperature *= 1 - cooling_rate
except KeyboardInterrupt:
if verbose:
timestamp = now = datetime.now().strftime("%H:%M:%S")
print(index, timestamp,
best_key, best_score, "Ended early due to KeyboardInterrupt")
return best_key, best_score, temperature
This function, together with digraph/trigraph scoring is able to crack Playfair ciphers, but it takes several minutes, even up to half an hour. We need it to be a lot faster.
Parallel
One obvious way to get more performance is to run many searches in parallel. I could have done this
the easy way and simply kicked off a number of independent searches each seeded with a different
random starting key, but I didn’t like the way most of the processes would be flailing around blindly
while one process ended up doing all the work. That meant implementing some coordination mechanisms
so that processes that weren’t having any luck would be recycled and used to “swarm” the current best
solution. This involved Python’s multiprocessing package to share locks and values across processes,
but it ended up being worth it. The swarming approach really made a huge difference in the total time
to find a correct solution.
def process_worker(args):
key, ciphertext, initial_temperature, cooling_rate, \
global_best, global_best_key, global_since, global_lock = args
log(2, f'Process {os.getpid()} started with key: {key}')
# initialize search
best_score = 0
best_key = key
since = 0
temperature = initial_temperature
while True:
# do the inner simulated annealing search
key, score, temperature = simulated_annealing_crack(
ciphertext,
PlayfairCipher,
playfair_score,
starting_key=key,
attempts=attempts_per_epoch,
temperature=temperature,
cooling_rate=cooling_rate,
restart_patience=restart_patience,
verbose=(log_level >= 3))
# compare to local best
if score > best_score:
best_score = score
best_key = key
since = 0
else:
since += 1
# if we've found the global best solution, brag about it
with global_lock:
if best_score > global_best.value:
global_best.value = best_score
global_best_key.value = best_key
log(2, f'Found new global best key: {best_key} score: {best_score}')
cipher = PlayfairCipher(best_key)
sample_length = ((terminal_width-46)//2)*2
sample_text = cipher.decrypt(ciphertext[:sample_length])
human_readable_score = 100 * best_score / perfect_score
log(1, f'{best_key} '
'{sample_text:<{terminal_width-46}} '
'{human_readable_score:.0f}%')
global_since.value = 0
else:
global_since.value += 1
# if no process have improved on the global best in a long time,
# it's time call it quits
if global_since.value > global_patience:
break
# if we haven't had any luck lately, let's do a restart.
# if the global score is pretty close to perfect, we'll want to swarm on that.
# if the current best score is pretty close to the global score, we'll use that.
# otherwise, start over from a completely random key.
if since > restart_epoch_patience:
global_gap = (perfect_score - global_best.value)/perfect_score
if random.random() < global_gap:
key = PlayfairCipher.make_random_key()
cipher = PlayfairCipher(key)
plain_text = cipher.decrypt(ciphertext)
score = playfair_score(plain_text)
temperature = initial_temperature
log(2, f'Restarting with random key: {key}')
else:
gap = (global_best.value - best_score) / global_best.value
if random.random() < gap:
key = global_best_key.value
score = global_best.value
log(2, f'Restarting with global best key: {key}')
else:
key = best_key
score = best_score
log(2, f'Restarting with own best key: {key}')
# since we're close, start at a lower temperature
temperature = initial_temperature / 3
since = 0
return best_score, best_key
def parallel_crack(
ciphertext,
initial_temperature=8e-5,
cooling_rate=None,
pool_size=None):
# default to the initial temperature and cooling rate choosen by hyperopt
if not cooling_rate:
cooling_rate = 1 - math.exp(math.log(0.003)/(32*attempts_per_epoch))
if not pool_size:
pool_size = cpu_count()
keys = [ PlayfairCipher.make_random_key() for i in range(pool_size) ]
with Manager() as manager:
global_best = manager.Value('f', 0.0)
global_best_key = manager.Value('s', keys[0])
global_since = manager.Value('i', 0)
global_lock = manager.Lock()
args = [
(key, ciphertext, initial_temperature, cooling_rate,
global_best, global_best_key, global_since, global_lock)
for key in keys ]
with Pool(pool_size) as worker_pool:
log(2, f'Started {pool_size} worker processes.')
solutions = worker_pool.map(process_worker, args)
return global_best_key.value, global_best.value
return solutions
Here is what the output typical run looks like. You can see the “percent english” column on the far right steadily ticking upwards, and you can see from the process ID in the second column that more than one process is contributing even in the final seconds of the crack, demonstrating the power of the swarming approach. Personally, I really enjoy watching recognizable words start to appear in the sample plaintext in the fourth column; it’s oddly hypnotic.
Cipher Text: VYFAOAMEUGUGMQEXNWCWWSCOBHMFZIQYWAUGYWMEWCXIEAHZLGLMNYAZMZIUQYAFQMWCZILGLTGUGLYWYPRLFAMVWRZNWCISRBINCWIPIVZMYCNYEANBCNM ZAFHSUGROMWMVQYVORILMKSBFIUQYQNSBVIVYVIBFKRFWDRIUQYOCIXUBXMWOXMACRYIUQYOSFMMVWYMVOMMFUGAQMXGUIVQYXICNAWNZMEBILMWYBLCOBM VYFAIXQYOSCTAWMHCIIRLZQYNICOMXLMWUMALMPBNFRGQYIXQYSQSOQAWOWCUGMEOKWMMVKCYOZMDTDMMLCOIBMZUGMYHTRLMNSVUGWRTHGUQYPROPAMRUR YACNSYBPYDTBTMCCKGVQYWYDOMZIUPYMGWMFYAMMXGUQYFNFMIURMGMRXYWXISHVUWAYMYLAWUGAQMXGSWBDRTHGUISUGBKMDFMMKYWYMEAVIMCEBRWUGWF RWUGAHAWOSIUEAFBMZOCUZUGAZMALTYEMLDVKCIYROFAZMSASVDAWAORCTWQRWUGROWFKSPRWAVIVYFAIXNPMZGSOSSVOAMNUGNFMFYWMLMDWAMDAGWRILW YWYMCLTGUMAYMMVFYNSACNIIXMDKCAGWAQYYOSREV 13:33:30 17896 LWFDCOPEIZMANQRHSKGYUBXTV YRWNPMNOTHTHRNFKAFDLBALZUSNLIERGBPTHSCNOLDTEPNYODHUORKRPROOTRGNWNRLDIR 23% 13:33:30 18092 WTPQMZLVOEFYKHXRNCGISBDAU LKHSQGUMAIAIQPMERTRPSRGVAYWXERTHQSAIFTUMPREXOUFOONETYLSOWEXITHSHPQPROW 24% 13:33:30 20452 YASDBPWEQZFLGTNMCHKORXUVI RDLYCBHPHEHEKPWULZLAEAMKSOFPBOPDAXHEAPHPALRVWSOEFLFCFBBWOPVXPDYLPKALQE 17% 13:33:34 17896 NVMWFXQTZIBASOYPRUDHLCEKG FAVYSBEUHEHEVTLTFMKVMOKAYPVWTZIAVOHEOFEUVKIZCSDIGKENFBOQWTTHIAYVTVVKTX 28% 13:33:39 17896 NOMWFXQTZIBASRYPVUDHLCEKG HAOYCQEUHEHEOTLTFMKOMRVCYPOWTZIAORHERFEUOKIZCSDIGKENFBRQWTTHIAYOTOOKTX 29% 13:33:43 17896 NOMFWXQTIZBASYRPVUHDLCEGK HAOYCQEUHEHEOTLTWFKOMRVCYPOMITIAORHERFEUOKZTCSDIKEENFBRQWTTHIAYOTOOKIX 29% 13:33:44 16908 EYABDOPWFLQHIXZKSGMRCNTUV NDWBWEKBTMTMKXBQTPTOPGKEYXXBXHHEATTMAPKBOTIHDYQXWRFRSNDIRXXTHEBWXKOTX 31% 13:33:53 20452 UEYNTOVXMGPBRFALQHKWZDSCI XERFGPVNTOTOVKYVTKIKHIZMRQNMICHEAGTOTHVNKIGSTBLSWOKOYEPIOCZTHEFRKVKIDL 31% 13:33:54 16908 OPWAFQHIZRCVTLUKSGXDEYMNB HSAWFWYBTDTDEINKMATOPGQEYRBWIHHEPWTDMPYBOTGZNOQITTNMENANIRTHEWAIEOTIR 34% 13:34:08 16908 KDGXSQRIZHCUTLVOFWAPEBMNY HPOWPWBYTDTDEINKMATOPGQCYRBWIRHEFWTDMPBYOTGZNOZITTNMNLXNIRTHEWOIEOTIH 34% 13:34:12 20452 UEYITPBRACOMXKGLQHNWZFDSV DTSBKPBFTOTOBMYMHNTGNVPGRQBQSUHENCTOTHBFGTKYIBLDWOQOHIPSOFYTHEBSMBGTFL 35% 13:34:14 9896 SMOADKNCFPBWRVIUYEGHZTLXQ WGAXMOOYHEHEDTGLMNNRBMOLIUANQBTHVMHEWNOYRNQVGOUQXETOMWSSTBHTHXATDRNQX 37% 13:34:19 9896 KNCFPSMOADBWRVIUYEGHZTLXQ WGXFMOOYHEHEDTGLTMNRBMLCIUANQBTHVMHEWMOYRNQVGOUQXETOTWSSTBHTHFXTDRNQX 39% 13:34:26 6440 ZKTUFPEMYONARSCBQGHWXVIDL DEKCECEPTHTHEGPVCBOCHCOFWGOTTXHEQCTHOHEPCOLVKEBUIWIOSPNKPTDTHECKGECOKB 46% 13:34:35 6440 WGPQHFTOVUSCXNLAMDEYRIBZK UEWSFDADTHTHEGDNSQSGRFXTKPATBRHERSTHAHADGSCBDYQKCHCYLEEREIKTHESWGEGSE 50% 13:34:42 13048 DIWZNQGKHPVTXUCEMOYBFLASR UERLXOEBTHTHEGOVZIXNZAXBYPELWDHEAOTHOZEBNXTWOFZSMIMTZBSWYIZTHELRGENXDH 54% 13:34:44 6440 DFZISKLWPRUXVTOHNQGBYAEMC UEANXCEATHTHEGAVQLERRZBRGBAIFZHELETHEKEARETFAYQDPNPAHAEFEIDTHENAGEREEV 57% 13:34:47 13048 HQGPZNWIBCYEMADSFRLOUVTKX UELELDEYTHTHEGDVCNBNNFZDNPERGCHEBETHENEYNBTCYMZPRPRAHNDPDGNTHEELGENBPH 60% 13:34:55 13048 FPDLBRSOIWEYAMNZUVTCQHXGK UADEDOANTHTHEGAQWBNBIRVWPKELTRHEONTHNSANBNGONYQUGTGIMEEVETSTHEEDGEBNE 60% 13:34:57 6440 WLRBFPICSOEMYNAQGHKDZTUVX UNXOFOEATHTHEGAZEBPRBPISRKALTPHEFETHEREARPTOANQUTMTIYMEETCTHEOXGERPQE 64% 13:35:00 13048 ISORWLBKCFGHDPQTUVXZMYNAE UNCERNEATHTHEGAZEOFRRIKRSBELTWHERETHESEARFTRANQUILITYMEETSTHEECGERFQF 79% 13:35:01 6440 BCDFLUVXZTHKPQGYNAEMSORWI UNDERNEATHTHEGAZEOFORIONSUELTWHERETHESEAOFTRANQUITIGYMEETSTHEEDGEOFF 83% 13:35:04 13048 ISORWLBCDFGHPKQTUVXZMYNAE UNDERNEATHTHEGAZEOFORIONSBELTWHERETHESEAOFTRANQUILITYMEETSTHEEDGEOFQF 85% 13:35:06 6440 BCDFLHKPQGUVXZTYNAEMSORWI UNDERNEATHTHEGAZEOFORIONSBELTWHERETHESEAOFTRANQUILITYMEETSTHEEDGEOFQF 87% Candidate solution found! Key: BCDFLHKPQGUVXZTYNAEMSORWI Bigraph/Trigraph Score: 87% Plain Text: UNDERNEATHTHEGAZEOFORIONSBELTWHERETHESEAOFTRANQUILITYMEETSTHEEDGEOFTWILIGHTLIESAHIDDENTROVEOFWISDOMFORGOTTENBYMANYCOVET EDBYTHOSEINTHEKNOWITHOLDSTHEKEYSTOUNTOLDPOWERASTHENORTHSTARSTANDSASTHESILENTSENTINELTHEPATHTOTHETROVEREVEALSITSELFONLYU NDERTHESILVERYGLOWOFTHEMOONATITSZENITHDECIPHERTHEWHISPERSOFTHEANCIENTCONSTELLATIONSLETTHEMGUIDEYOUTHROUGHTHEDARKNESSAND YOUSHALLUNLOCKTHESECRETSTHATLIEBENEATHTHECELESTIALTAPESTRYBUTREMEMBERTHEPATHISFRAUGHTWITHCHALLENGESMEANTONLYFORTHEWORTH YPERSISTANDLETNOTTHEENIGMATICCOSMOSDETERYOURRESOLVEFORTHOSEWHODARETOUNDERTAKETHISIOURNEYTHECELESTIALREALMPROMISESENLIGH TENMENTBEYONDMORTALCOMPREHENSION Segmented Plain Text: UNDERNEATH THE GAZE OF ORIONS BELT WHERE THE SEA OF TRANQUILITY MEETS THE EDGE OF TWILIGHT LIES A HIDDEN TROVE OF WISDOM FORGOTTEN BY MANY COVETED BY THOSE IN THE KNOW IT HOLDS THE KEYS TO UNTOLD POWER AS THE NORTHSTAR STANDS AS THE SILENT SENTINEL THE PATH TO THE TROVE REVEALS ITSELF ONLY UNDER THE SILVERY GLOW OF THE MOON AT ITS ZENITH DECIPHER THE WHISPERS OF THE ANCIENT CONSTELLATIONS LET THEM GUIDE YOU THROUGH THE DARKNESS AND YOU SHALL UNLOCK THE SECRETS THAT LIE BENEATH THE CELESTIAL TAPESTRY BUT REMEMBER THE PATH IS FRAUGHT WITH CHALLENGES MEANT ONLY FOR THE WORTHY PERSIST AND LET NOT THE ENIGMATIC COSMOS DETER YOUR RESOLVE FOR THOSE WHO DARE TO UNDERTAKE THIS I OUR NEY THE CELESTIAL REALM PROMISES ENLIGHTENMENT BEYOND MORTAL COMPREHENSION English Word Score: 91% Accepted solution.
At the end, you can see the word segmentation and “percent English” functions evaluating the final cracked plaintext; if this check fails, the whole process simply resets from scratch. (Due to the randomization involved, it does sometimes get stuck, and resetting is often the kindest thing we can do.) That means you can simply “fire and forget” and trust the algorithm and its “sense of rightness” to know when the cipher has been successfully cracked.
However, even with parallelization, (which gives me a 12x speed-up on this machine, and theoretically a lot more if I rented a beefy AWS compute instance) this is still taking minutes to crack, not seconds. So let’s see what other optimizations we can make.
Cython
Python is very slow at character-by-character string manipulation. Unfortunately,
that’s exactly what the inner loop of Playfair.decrypt() is doing. We can use Cython
to optimize the performance critical section of the code:
@cython.boundscheck(False)
@cython.wraparound(False)
cpdef str playfair_decrypt(str cipher_text, str key):
"""
Decrypt the given cipher text using the Playfair cipher with the provided key.
Arguments:
cipher_text -- The encrypted text. Must contain an even number of uppercase letters.
key -- The key for decryption. Must be exactly 25 uppercase letters.
Returns:
The decrypted text.
"""
cdef int i, j
cdef int n = len(cipher_text)
# populate a reverse lookup table
cdef int[25][2] reverse_lookup
for i in range(25):
j = playfair_ord(key[i])
reverse_lookup[j][0] = i // 5
reverse_lookup[j][1] = i % 5
# Allocate memory for the result
cdef char* decrypted_text = <char*>malloc(n+1)
if not decrypted_text:
raise MemoryError()
# decrypt playfair cipher
cdef int x1, x2, y1, y2
try:
# Loop over the characters in cipher_text
for i in range(0, n, 2):
x1, y1 = reverse_lookup[playfair_ord(cipher_text[i])]
x2, y2 = reverse_lookup[playfair_ord(cipher_text[i+1])]
if x1 == x2:
decrypted_text[i] = key[5*x1 + (y1-1)%5]
decrypted_text[i+1] = key[5*x2 + (y2-1)%5]
elif y1 == y2:
decrypted_text[i] = key[5*((x1-1)%5) + y1]
decrypted_text[i+1] = key[5*((x2-1)%5) + y2]
else:
decrypted_text[i] = key[5*x1 + y2]
decrypted_text[i+1] = key[5*x2 + y1]
# Null-terminate the string
decrypted_text[n] = b'\0'
# Convert the byte array back to a Python string to return it
return decrypted_text.decode('utf-8')
finally:
# Free the allocated memory
free(decrypted_text)
This worked like magic and resulted in a significant speed-up. It did have some downsides; this version is extremely brittle and will segfault if the input ciphertext or key do not exactly match what it expects - for example, if the ciphertext is an odd number of characters. You’ll notice that is largely my own fault - I’m explicitly turning off bounds checking for example - but could easily be avoided by implementing a few simple sanity checks before entering the hot, Cython optimized, section of the code. Because in theory the ciphertext is coming from the wild, I thought it would be useful to write these sanity checks in a user-friendly way so that any problems in the ciphertext (which may indeed indicate that the ciphertext isn’t from Playfair at all, but some other algorithm entirely) can be reported to the user:
def playfair_ciphertext_violations(text: str) -> list:
violations = []
other_characters = len(re.findall(r'[^a-ik-zA-IK-Z\s]', text))
if other_characters:
violations.append(
f"Text contains {other_characters} characters not used by Playfair.")
text = scrub(text)
# Check for even length
if len(text) % 2 != 0:
violations.append("Text length is not even.")
# Check for double letters
double_letters = 0
for digraph in pairs(text):
if len(digraph) == 2:
if digraph[0] == digraph[1]:
double_letters += 1
if double_letters:
violations.append(
f"Text contains {double_letters} invalid double letters.")
# Check for more than 25 unique characters
unique_characters = len(set(text))
if unique_characters > 25:
violations.append(
f"Text contains {unique_characters} unique letters, "
"more than the 25 used by Playfair ciphers.")
# check for letter J
if 'J' in text:
violations.append(
"Text contains letter 'J', which is not used by Playfair ciphers.")
# Check for ciphertext length
length = len(text)
if length < 100:
violations.append(
f"Text contains only c{length} characters and may be too short to crack.")
return violations
Hyperparameter Optimization
While I’m very happy with the parallelization and Cython micro-optimization, I still have a nagging doubt about the simulated annealing algorithm itself. You see, I had to specify a number of parameters, the most important of which was the temperature schedule. I played around a little by hand to make sure the values weren’t crazy, but the algorithm was so slow back then that I really only tried a handful of values. Now that the algorithm is fairly performant, this is the perfect time to go back and make sure we’re using the best possible hyperparameters.
To do this, we’ll use one of my favorite libraries, hyperopt. Hyperopt also uses derivative-free optimization, but it takes a different approach than simulated annealing. It uses a Bayesian approach to construct a Gaussian process proxy function to approximate the true function being optimized, and uses that proxy function to guide its search towards the most promising regions of the hyperparameter space.
You may be wondering why I chose a completely different algorithm for this part, when I’d already used simulated annealing to solve a very similar problem above. The reason is that in this case, evaluating the true objective function is very expensive - 30 seconds instead of milliseconds - and the hyperparameter space is low-dimensional and continuous instead of high-dimensional and discrete. So while the optimization problems are technically in the same category, the specifics of each problem lead to a different choice of algorithm.
Here is the inner core of the objective function, where we simply attempt the crack with specified parameters:
def crack(ciphertext, params):
for _ in range(MAX_ATTEMPTS):
key, score = mp.parallel_crack(
ciphertext,
initial_temperature=params['initial_temperature'],
cooling_rate=params['cooling_rate']
)
score, english = evaluate(ciphertext, key)
if english > mp.acceptance_threshold:
break
return key, score, english
Note that we’re actually optimizing for how quickly we can crack the cipher; we’ll measure the clock time it takes to run, and use that as the “loss” returned from the objective function.
def objective(params):
for i in range(N_REPEATS):
# create a new problem each repeat
true_key = PlayfairCipher.make_random_key()
cipher = PlayfairCipher(true_key)
ciphertext = cipher.encrypt(plaintext)
# measure time to crack
start_time = time.time()
key, score, english = crack(ciphertext, params)
end_time = time.time()
duration = end_time - start_time
# hyperopt boilerplate omitted
return {
'loss': df['duration'].mean(),
'loss_variance': df['duration'].var(),
'status': STATUS_OK,
# other metrics omitted
}
With our objective function fleshed out, let’s ask hyperopt to find us the optimal parameters:
def hyperoptimize(trials=None):
if trials is None:
trials = Trials()
space = {
'initial_temperature': hp.loguniform(
'initial_temperature',
low=np.log(1e-5),
high=np.log(1e-3)),
'cooling_rate': hp.loguniform(
'cooling_rate',
low=np.log(0.0001),
high=np.log(0.0003)),
}
best = fmin(
fn=objective,
space=space,
algo=tpe.suggest,
trials=trials,
max_evals=N_TRIALS)
return best, trials
It looks like there is a clear but not particularly strong minimum:
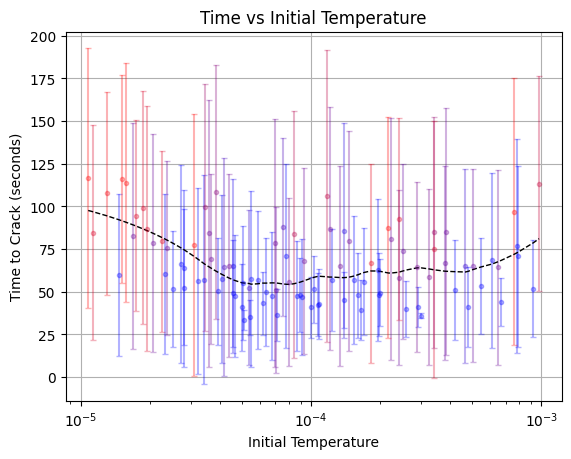
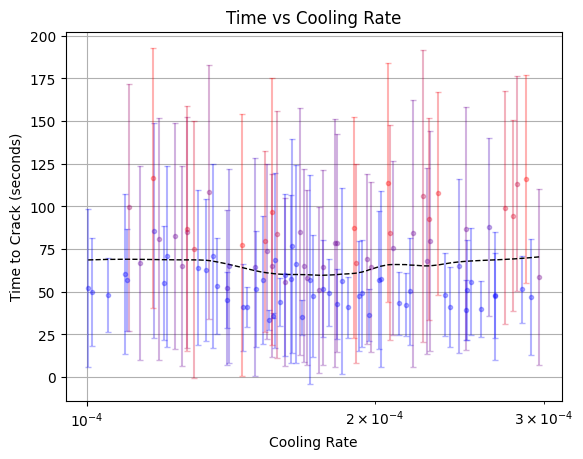
That’s okay; hyperparameter optimization is often more about having confidence that you haven’t left any easy wins on the table than finding some secret combination of hyperparameters that magically give you 10X performance.
Conclusion
It’s clear that the “microseconds” used in the Wikipedia article is hyperbole. That’s only enough time to try a handful of keys, and Playfair is not so weak that you can zero in on the solution that quickly. Nor is the problem “embarrassingly parallel” - you can run lots of parallel attacks across a large server farm, but you can’t run $24!$ separate processes, or even make a dent in it with brute force. You have to use something clever like simulated annealing or constraint solving, and those are fundamentally sequential.
Still, the Playfair cipher is indeed quite weak - an amateur cryptographer with a desktop and a couple of free weekends can write a program which will crack it in under a minute. Don’t use it for your important secrets! But do use it for fun and games, as it’s delightful.
One surprising thing I learned is that ChatGPT can solve the word segmentation problem quite well, and it can even add punctuation and capitalization back into the message. While LLMs are far too slow to participate in the performance-intensive crack (we can use simpler heuristics like trigrams for that,) their ability to make semantic sense of partially mangled text might still be useful in automating the “sense of rightness” which hitherto has been left to human cryptographers.