
The Art and Mathematics of Genji-Kō
You might think it’s unlikely for any interesting mathematics to arise from incense appreciation, but that’s only because you’re unfamiliar with the peculiar character of Muromachi (室町) era Japanese nobles.
There has never been a group of people, in any time or place, who were so driven to display their sophistication and refinement. It wouldn’t do to merely put out a few sticks of incense; no, you would have to prove that your taste was more exquisite, your judgment more refined, your etiquette more oblique. You could of course merely invite some other nobles over for an incense appreciation party, make a few cutting but plausibly deniable remarks about a rival, maybe drop a few lines of poetry linking the incense to the current season. But if you were really on the ball you’d be looking for a way to simultaneously humiliate your rivals, flirt with your love interest, and impress people in a position of power. They didn’t just perfect cultured refinement: they weaponized it.
Only under such conditions could something like Genji-kō (源氏香) arise. It is a parlor game played with incense—just one of many similar games inside the broader umbrella of kōdō (香道), the traditional Japanese art of incense appreciation.
What sets Genji-kō apart is its extreme difficulty. While another kōdō game might have contestants write down their guesses for three separate incenses and score a point for each correct guess, Genji-kō asks contestants to smell five separate samples, then determine which of the five were the same scent. All five might be the same, all five might be different, or (and this is where it gets interesting) they might be in groups of two or three or four.
Contestants score a single point by correctly guessing all five incenses; otherwise they score nothing. A typical game has five rounds over the course of an evening, with an overall winner declared at the end.
Obviously contestants would need some kind of notation to submit their answers in a concise and unambiguous way, and it is really about this notation (and the art, mathematics, and culture connected to it) that this article is about.
Notation
The solutions that Genji-kō players submit are called Genji-mon (源氏紋) and are drawn with exactly five vertical lines, representing the five possible incenses. To show that two or more incenses are part of the same group, you draw a horizontal line connecting the top of every vertical line in that group. To avoid confusion when there are two or more groups, you draw these horizontal lines at different heights, shortening the vertical lines as needed:
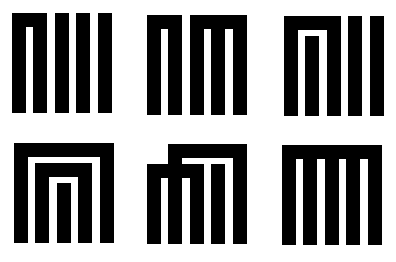
There are a few nuances worth mentioning. If two groups don’t overlap, there is no need to draw them at different heights (top center.) Sometimes it is impossible to avoid an intersection (bottom center) but it is clear that groups are distinct because the horizontal connecting lines are at different heights; nevertheless, we try to minimize such intersections.
Genji-kō features as a plot point in episode 8 of the experimental horror anime Mononoke, where it is suggested that players used blocks to record their solutions:
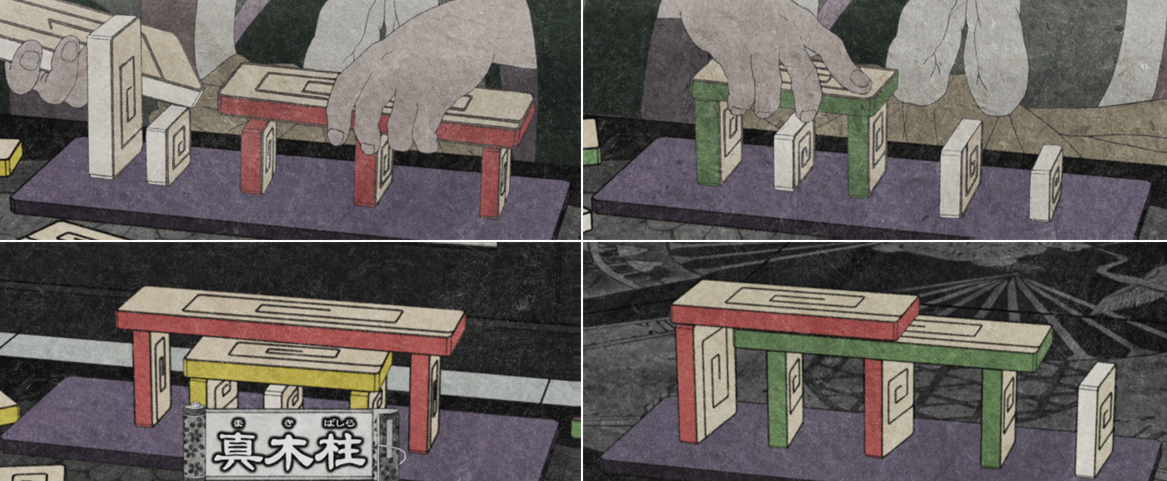
While this might be true - the episode’s description of Genji-kō is otherwise grounded and well-researched - I haven’t seen any other references to this; everything else I’ve seen indicates the game was played with ink and paper. I think it’s probably just a case of artistic license.
Etymology
Genji-kō, by the way, is named after the titular Genji of the Heian (平安) era literary classic The Tale of Genji. (The fact that “Genji” is a proper name is also why I capitalize Genji-kō and Genji-mon.)
There are two connections. First, in one chapter of the book Genji hosts an incense appreciation party. Second, since there are 52 possible patterns and 54 chapters of the book, each Genji-mon is traditionally associated with—and named after—a chapter, except for the first and last chapters, which are omitted.
Every educated person of the Muromachi era would have been be intimately familiar with The Tale of Genji and would know the themes, season, and characters associated with each chapter by heart, giving each pattern a literary resonance. A skillful kōdō practitioner hosting a game of Genji-kō would choose a solution that referenced the current season or recent event, adding both a additional layer of meaning to the game and a hint to skilled players.
There are several different words we could use to refer to the patterns themselves, but I’ve chosen Genji-mon as it seems to be the most common.
Cultural Influence
Compared to other traditional arts from the same era such as tea ceremony or flower arranging, kōdō is not particularly popular or well-known, even in Japan; nevertheless it is still played even to this day.
However, its cultural influence extends beyond the few who actually play the game - the patterns show up fairly often as motifs in contemporary Japanese graphic design, and it’s especially popular on traditional goods such as kimono:


While cheaper fabrics simply print the same Genji-mon repeatedly, high-quality Genji-kō textiles will use a variety of Genji-mon so that the pattern seems to never quite repeat:

Naturally, Genji-mon are often found on goods related to incense in some way, such as this kōdō set, incense box, or incense holder:



In the 1840s Kunisada painted a series of wall scrolls, one for each chapter of The Tale of Genji, and included the associated Genji-mon on each:
Drawing Genji-Mon
To draw Genji-mon programmatically, we’ll use the standard recursive algorithm to generate all possible partitions for a set of five elements:
def partitions(s: Set[int]) -> Iterator[List[Set[int]]]:
"""Yield all partitions of a set as they are generated."""
if not s:
yield []
return
first = next(iter(s))
rest = s - {first}
for partition in partitions(rest):
yield [{first}] + partition
for i in range(len(partition)):
new_partition = (
partition[:i] +
[partition[i] | {first}] + partition[i+1:]
)
yield new_partition
However, the partition alone does not suffice to fully characterize a Genji-mon. While we must draw overlapping groups at different heights to avoid ambiguity, there is still a free choice about which groups we make taller. After studying the chart of traditional Genji-mon, two rules became clear:
- Groups should be as tall as possible.
- Groups entirely inside† other groups should be lower and appear to nest inside the outer group.
I implemented this as a simple brute-force cost-based optimizer, because that made it easy to experiment with different rules. (Even though in the end I only used those two simple rules, I experimented with many others trying to get rid of the remaining special cases, which I’ll discuss below.)
def optimal_genjiko_for_partition(
partition: List[Set[int]]
) -> List[Tuple[float, Set[int]]]:
"""
Given a partition, find the optimal Genji-kō layout by minimizing a cost
function.
"""
best_cost = math.inf
best_genjiko = None
HEIGHTS = [1.0, 0.8, 0.6]
# Generate all possible combinations of heights
for height_combo in itertools.product(HEIGHTS, repeat=len(partition)):
genjiko_candidate = [
(height, group)
for height, group
in zip(height_combo, partition)
]
# Skip invalid configurations
if not validate_genjiko(genjiko_candidate):
continue
# Encourage larger heights
cost = -sum(height for height, _ in genjiko_candidate)
for height1, group1 in genjiko_candidate:
for height2, group2 in genjiko_candidate:
# Large penalty for higher inner group height
if is_nested_within(group1, group2) and height1 > height2:
cost += 1
# keep track of the best solution so far
if cost < best_cost:
best_cost = cost
best_genjiko = genjiko_candidate
return best_genjiko
Drawing these using Pillow or organizing them into a grid is straight-forward, so you can check the source code if you’re interested in those details.
Here’s what we get if we always use the algorithmically calculated “optimal”
layout and simply put them in the order returned by partitions():

Good, but not perfect. The order is only vaguely similar, and the four Genji-mon rendered in red are the ones where our “optimal” layout has failed to reproduce the traditional design.
Genji-mon Order
In the introduction he wrote for a book on ancient combinatorics, Knuth
mentions
that the Genji-mon “were not arranged in any particularly logical order” and
I’m inclined to agree. I tried several variations of the above partitions()
function hoping to find one where the traditional order would just fall out
naturally, but it never did. A close inspection of the traditional order makes
it clear that this was never going to happen: While there is an overall trend
from many to fewer groups, there are just too many cases where the order is
clearly arbitrary.
I found several references that put them in a different order, and even some that tried to stretch it to 54 using some kind of duplication or introducing irregular patterns.* However, if we recall what the notation is designed to represent this is clearly nonsense: simultaneously useless for playing Genji-kō, mathematically impossible, and at odds with tradition.
However, the association between the 52 patterns and chapter titles for chapters 2-53 of the Tale of Genji seems watertight and consistent for centuries back. Also, the order of the chapters is mostly consistent across sources (there is some disagreement about the order of the later chapters, and one chapter which survives only as a title or perhaps was intentionally elided as a delicate way to allude to a certain character’s death) so I’ve put my Genji-mon in chapter order following Waley. You can find the full table in Appendix C.
Special Cases
I spent some time trying to find some elegant heuristic that would nudge the layout algorithm to produce those four without breaking any of the others, but the rules were more complex than simply listing the special cases (and none of them correctly handled Yūgiri (夕霧), which I’ll discuss below.)
The four special cases are:
# Suma: {1, 3, 4} should be lower than {2, 5}
df.at[10, "Layout"] = [ (0.8, {1, 3, 4}), (1.0, {2, 5}) ]
# Hatsune: {1, 3} should be lower than {2, 4}
df.at[21, "Layout"] = [ (0.8, {1, 3}), (1.0, {2, 4}), (1.0, {5}) ]
# Yugiri: {1, 4} should be lower than {3, 5}, and {2} even lower.
df.at[37, "Layout"] = [ (0.8, {1, 4}), (0.6, {2}), (1.0, {3, 5}) ]
# Nioumiya: {1, 2, 4} should be lower than {3, 5}
df.at[40, "Layout"] = [ (0.8, {1, 2, 4}), (1.0, {3, 5}) ]
With these corrections, and using the Tale of Genji chapter order:

Of the four exceptions, two are obvious improvements (fixing the “hole” in Suma and the “dent” in Hatsune), and one (Nioumiya) is a matter of indifference. However, the fourth, Yūgiri, seems to violate the most basic rule of nesting and creates a three-level structure when two would have sufficed:

The cost-based optimizer would never have chosen that layout because its most basic tenet is to make the groups as tall as possible. A heuristic, let me remind you, that holds for the other 51 Genji-mon. However, all the examples of Yūgiri I found online use the traditional design, such as the wall scroll by Kunisada or this woodblock print by Masao Maeda:
So I don’t think I have a leg to stand on unless I want to fly in the face of hundreds of years of tradition; we’ll just have to hard-code Yūgiri as a special case.
Counting Genji-Mon
The connection between Genji-kō and mathematics becomes apparent if we ask ourselves, “Why are there exactly 52 Genji-mon patterns? How can we be sure there aren’t more?”
Like a lot of questions in mathematics, it helps to generalize things. Instead of focusing on five incenses, let’s ask ourselves, how many unique ways are there of grouping $n$ elements? This approach lets us ease into the problem, starting with a simpler case and building complexity gradually.
For $n = 1$, there’s clearly only one solution:

For $n = 2$, there are only two possible solutions. Either the first element is in a group by itself, or it is in a group with another.

For $n = 3$, things start to get more interesting. Let’s focus on the first element. It must either be in a group by itself, in a pair with another, or in the same group as all others. That gives us exactly three cases to consider:
- If the first element in a group by itself, then there are two elements left over; we showed above that there are two ways to partition those.
- If it’s in a pair, then we have a choice: we can either pair it with the second or third element. In either case there will only be one element left over.
- And there is only one way to have all the elements be in the same group.
Here they all are, in Genji-kō notation:

Thus, we have $1 \times 2 + 2 \times 1 + 1 = 5$ ways to partition a set of three elements.
This is starting to look like a repeatable strategy. We always start by focusing on the first element. We then divide up the set of all possible solutions by the size $k$ of the group containing this first element. For each $k$ between $1$ and $n$, there are two questions to ask:
- How many ways are there of choosing the set that contains the first element?
- How many ways are there of putting the remaining $n-k$ elements into groups?
Let’s try that out for $n = 4$. The other cases are obvious, but let’s go into more depth for the case where $k = 2$ as there’s a new wrinkle there. We have to choose one other element from three possible elements, so there are three ways of doing that. We’ll always have two left over, and there are always two ways of grouping those together. These are two independent choices: we choose the first group, then choose how to partition the remaining elements. Because they are independent, we multiply to find there are $3 \times 2 = 6$ ways of putting them together.
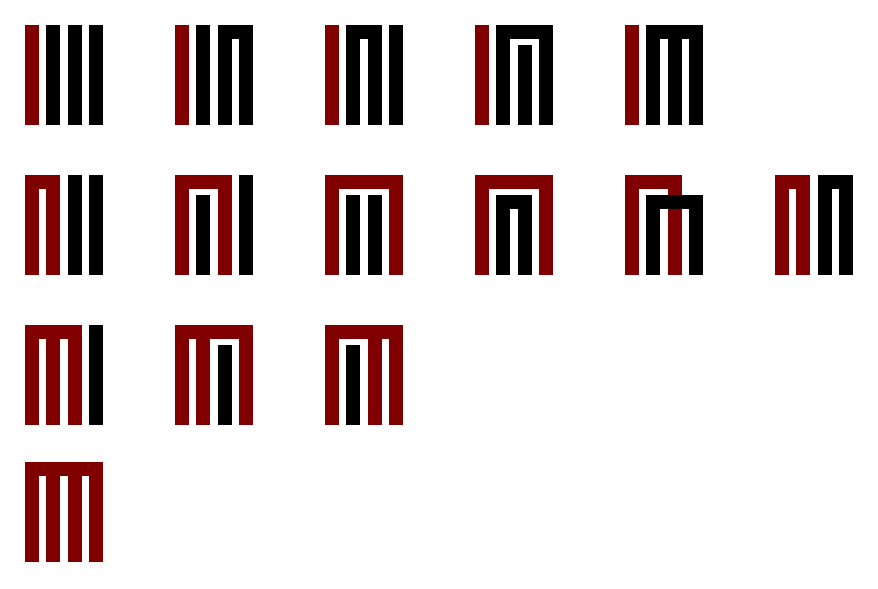
So, for $n = 4$, there are $1 \times 5 + 3 \times 2 + 3 \times 1 + 1 = 15$ possible solutions.
Mathematical Approach
For the case of $n = 5$, I’ve generated the diagram showing how to use the same strategy to count all possible Genji-mon, but I think it’s more useful to take the strategy we’ve learned and abstract it.
First, let’s use the right terminology. What we’ve so far called a “Genji-mon,” mathematicians would call a partition. In mathematical terms, the question we’re asking is, “How many distinct partitions are there for a set of $n$ elements?” This number also has a name: the Bell number denoted $B_n$.
Above, we calculated $B_1$ through $B_4$ using a mix of intuition and common sense. To formalize the strategy we used in mathematical notation we’ll need a concept you may or may not have seen before: “the number of ways to choose $k$ elements from $n$ distinct elements, ignoring order” is called “$n$ choose $k$” or the binomial coefficient and is denoted with this tall bracket notation:
\[ \binom{n}{k} = \frac{n!}{k! (n-k)!} \]
There are many ways of deriving this equation, but here’s one I like: imagine we put all $n$ elements in order; there are $n!$ ways of doing that. Then we always take the $k$ leftmost elements for our choice. However, because order doesn’t matter, we divided by all the different ways of ordering the $k$ chosen elements, which is $k!$, and the $n-k$ remaining elements, which is $(n-k)!$.
With that tool in hand, we can define the Bell numbers recursively. The first couple can be treated as special cases, since obviously there’s only one way to partition a set of zero or one elements:
\[ B_0 = 1, B_1 = 1 \]
For $n > 1$, we generalize the strategy we discovered above:
- Pick an arbitrary element to represent the “first element.”
- We’ll call whichever set in the partition that contains this first element the “first set.” Every element is in exactly one set of the partition, so this uniquely picks out a particular set in the partition.
- For each $k$ between $1$ and $n$, consider only partitions where the first set is of size $k$. This divides the problem up into non-overlapping buckets: if two partitions have different sized first set, they cannot possibly be the same.
- We have to make a choice about the other $k-1$ elements to include in the first set, and there are $\binom{n-1}{k-1}$ ways of doing that.
- Regardless of which elements we choose for the first set, there will always be $n-k$ elements left over. They won’t always be the same elements, but there will always be $n-k$ of them. Thankfully, we already know how many ways there are to partition a set of $n-k$ elements: it’s $B_{n-k}$.
- Since our choices for step 4 and step 5 are independent, we can multiply the two counts together to get the total number of partitions where the first set is of size $k$.
- Finally, we just have to add up everything for $k$ from $1$ to $n$.
In concise mathematical notation, this algorithm is:
\[ B_{n} = \sum_{k=1}^{n} \binom{n-1}{k-1} B_{n-k} \tag{1} \]
We can make this a little neater if we run $k$ from $0$ to $n-1$ instead and use the fact that $\binom{n}{r} = \binom{n}{n-r}$ to count down instead of up:
\[ B_{n} = \sum_{k=0}^{n-1} \binom{n-1}{k} B_{k} \tag{2} \]
Substituting $n+1$ for $n$ we can put the recurrence relation in an even tidier form, which is the canonical form you’ll find in textbooks:
\[ B_{n+1} = \sum_{k=0}^n \binom{n}{k} B_k \tag{3} \]
Equation $(3)$ looks a little cleaner and easier to work with, and can be understood intuitively if you reconceptualize $k$ not as the number of elements in the first group, but as the number of elements not in the first group. Shifting to calculating $B_{n+1}$ also allows us to get rid of the “minus ones” in the original that made the expression seem messy. However, it’s a little divorced from the intuition about pinning the size of the first set we used to motivate $(1)$ although of course they’re completely equivalent mathematically.
Computing Bell Numbers
Of these three equivalent equations, $(2)$ is the most natural fit for a Python
implementation because range(n) naturally runs from 0 to n-1 and it makes
far more sense to implement a function for $B_n$ instead of $B_{n+1}$:
def bell_number(n: int) -> int:
"""Calculate the Bell number for any integer `n`."""
if n < 0:
raise ValueError("The Bell number is not defined for n < 0.")
elif n < 2:
return 1
else:
return sum(
comb(n-1, k) * bell_number(k)
for k in range(n)
)
(Optimizing this function is left as an exercise to the reader, who may find the techniques described in my earlier article on writing a fairly fast Fibonacci function helpful.)
We can use it to calculate the first 20 Bell numbers:
| $n$ | $B_n$ |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 5 |
| 4 | 15 |
| 5 | 52 |
| 6 | 203 |
| 7 | 877 |
| 8 | 4,140 |
| 9 | 21,147 |
| 10 | 115,975 |
| 11 | 678,570 |
| 12 | 4,213,597 |
| 13 | 27,644,437 |
| 14 | 190,899,322 |
| 15 | 1,382,958,545 |
| 16 | 10,480,142,147 |
| 17 | 82,864,869,804 |
| 18 | 682,076,806,159 |
| 19 | 5,832,742,205,057 |
| 20 | 51,724,158,235,372 |
And there it is: $B_5 = 52$, confirming that there are exactly 52 Genji-mon, no more and no fewer.
Conclusion
It’s not too surprising that some of these ideas were worked out over seven hundred years ago; combinatorics is an easy branch to stumble into when it arises in connection to some practical problem. It does, however, feel slightly surreal that it was a bunch of bored nobles playing an esoteric parlor game who first noticed these patterns and used it to attach literary significance to their activities. But I’m glad they did so, because they did something we mere number crunchers would not have thought to do: they made them beautiful.
Appendix A: Source Code
The full source code use for this article is available on GitHub. The main Python code is in src/genjiko.py and the notebooks directory contains many examples of usage.
Appendix B: Alternative Genji-Kō Chart
Genji-mon are often rendered with thick lines which achieves an interesting effect with the negative space. By playing around with the parameters a little:
genjiko_df = load_genjiko()
genjiko_df['Color'] = "black"
draw_annotated_genjiko_grid(
genjiko_df,
cell_size=82,
grid_width=8,
grid_height=7,
line_width=14,
padding=20,
include_index_label=False,
include_romaji_label=False,
grid_indent=1,
)
We can achieve a very attractive result:

Appendix C: Full Table
Here is the full table in HTML format, so you can copy-and-paste the kanji and other fields. The Genji-mon column uses the Genji-Kō TrueType font available from illllli.com.
You can also download this same table as a UTF-8 encoded CSV file or Excel spreadsheet.
| Chapter | Kanji | Romaji | English | Partition | Genji-mon |
|---|---|---|---|---|---|
| 2 | 帚木 | Hōkigi | The Broom Tree | {1}, {2}, {3}, {4}, {5} | B |
| 3 | 空蝉 | Utsusemi | Utsusemi | {1}, {2}, {3}, {4, 5} | C |
| 4 | 夕顔 | Yūgao | Yūgao | {1}, {2}, {3, 4}, {5} | D |
| 5 | 若紫 | Wakamurasaki | Young Murasaki | {1}, {2, 3}, {4, 5} | E |
| 6 | 末摘花 | Suetsumuhana | The Saffron Flower | {1, 2, 3, 4}, {5} | F |
| 7 | 紅葉賀 | Momijinoga | The Festival of Red Leaves | {1}, {2, 3, 5}, {4} | G |
| 8 | 花宴 | Hana no En | The Flower Feast | {1}, {2}, {3, 5}, {4} | H |
| 9 | 葵 | Aoi | Aoi | {1, 2}, {3}, {4}, {5} | I |
| 10 | 賢木 | Sakaki | The Sacred Tree | {1, 2, 3}, {4, 5} | J |
| 11 | 花散里 | Hana Chiru Sato | The Village of Falling Flowers | {1}, {2, 4}, {3, 5} | K |
| 12 | 須磨 | Suma | Exile at Suma | {1, 3, 4}, {2, 5} | L |
| 13 | 明石 | Akashi | Akashi | {1}, {2, 3}, {4}, {5} | M |
| 14 | 澪標 | Miotsukushi | The Flood Gauge | {1}, {2, 4, 5}, {3} | N |
| 15 | 蓬生 | Yomogiu | The Palace in the Tangled Woods | {1, 2, 3}, {4}, {5} | O |
| 16 | 関屋 | Sekiya | A Meeting at the Frontier | {1}, {2, 3, 4}, {5} | P |
| 17 | 絵合 | Eawase | The Picture Competition | {1, 3}, {2, 5}, {4} | Q |
| 18 | 松風 | Matsukaze | The Wind in the Pine Trees | {1, 2}, {3, 4}, {5} | R |
| 19 | 薄雲 | Usugumo | A Wreath of Cloud | {1}, {2, 3, 4, 5} | S |
| 20 | 朝顔 | Asagao | Asagao | {1, 3, 4}, {2}, {5} | T |
| 21 | 乙女 | Otome | The Maiden | {1, 3}, {2}, {4}, {5} | U |
| 22 | 玉鬘 | Tamakazura | Tamakatsura | {1, 2}, {3, 4, 5} | V |
| 23 | 初音 | Hatsune | The First Song of the Year | {1, 3}, {2, 4}, {5} | W |
| 24 | 胡蝶 | Kochō | The Butterflies | {1, 4}, {2, 3, 5} | X |
| 25 | 蛍 | Hotaru | The Glow-Worm | {1, 2, 4}, {3}, {5} | Y |
| 26 | 常夏 | Tokonatsu | A Bed of Carnations | {1}, {2}, {3, 4, 5} | Z |
| 27 | 篝火 | Kagaribi | The Flares | {1}, {2, 4}, {3}, {5} | a |
| 28 | 野分 | Nowaki | The Typhoon | {1, 2}, {3}, {4, 5} | b |
| 29 | 御幸 | Miyuki | The Royal Visit | {1, 3}, {2, 4, 5} | c |
| 30 | 藤袴 | Fujibakama | Blue Trousers | {1, 4}, {2}, {3}, {5} | d |
| 31 | 真木柱 | Makibashira | Makibashira | {1, 5}, {2, 4}, {3} | e |
| 32 | 梅枝 | Umegae | The Spray of Plum Blossom | {1, 2, 3, 5}, {4} | f |
| 33 | 藤裏葉 | Fuji no Uraba | Fuji no Uraba | {1}, {2, 5}, {3, 4} | g |
| 34 | 若菜上 | Wakana Jō | Wakana, Part I | {1, 2, 5}, {3, 4} | h |
| 35 | 若菜下 | Wakana Ge | Wakana, Part II | {1, 3}, {2}, {4, 5} | i |
| 36 | 柏木 | Kashiwagi | Kashiwagi | {1, 3, 5}, {2}, {4} | j |
| 37 | 横笛 | Yokobue | The Flute | {1, 4, 5}, {2}, {3} | k |
| 38 | 鈴虫 | Suzumushi | The Bell Cricket | {1, 5}, {2}, {3, 4} | l |
| 39 | 夕霧 | Yūgiri | Yūgiri | {1, 4}, {2}, {3, 5} | m |
| 40 | 御法 | Minori | The Law | {1, 4}, {2, 5}, {3} | n |
| 41 | 幻 | Maboroshi | Mirage | {1, 5}, {2}, {3}, {4} | o |
| 42 | 匂宮 | Nioumiya | Niou | {1, 2, 4}, {3, 5} | p |
| 43 | 紅梅 | Kōbai | Kōbai | {1}, {2, 5}, {3}, {4} | q |
| 44 | 竹河 | Takekawa | Bamboo River | {1, 5}, {2, 3, 4} | r |
| 45 | 橋姫 | Hashihime | The Bridge Maiden | {1, 3, 4, 5}, {2} | s |
| 46 | 椎本 | Shiigamoto | At the Foot of the Oak Tree | {1, 4}, {2, 3}, {5} | t |
| 47 | 総角 | Agemaki | Agemaki | {1, 4, 5}, {2, 3} | u |
| 48 | 早蕨 | Sawarabi | Fern Shoots | {1, 2}, {3, 5}, {4} | v |
| 49 | 宿木 | Yadorigi | The Mistletoe | {1, 2, 4, 5}, {3} | w |
| 50 | 東屋 | Azumaya | The Eastern House | {1, 2, 5}, {3}, {4} | x |
| 51 | 浮舟 | Ukifune | Ukifune | {1, 5}, {2, 3}, {4} | y |
| 52 | 蜻蛉 | Kagerō | The Gossamer Fly | {1, 3, 5}, {2, 4} | z |
| 53 | 手習 | Tenarai | Writing Practice | {1, 2, 3, 4, 5} | 1 |
Note that whenever the English column has apparently been left untranslated, this is because the chapter title is the proper name of one of the characters from The Tale of Genji. Translating these would be as nonsensical as translating “Jack Smith” to “Lifting Device Metal Worker.”
Appendix D: Names for Genji-Kō Pattern
This table is included merely to illustrate the variety of legitimate ways to refer to the patterns used in Genji-kō, and to justify my choice to standardize on Genji-mon. Click on any of the kanji to link directly to the Google Image Search for that name.
| Kanji | Romaji | English Translation | Count |
|---|---|---|---|
| 源氏紋 | Genji-mon | Genji Crest | 844,000 |
| 源氏香図 | Genji-kōzu | Genji-kō Diagram | 686,000 |
| 源氏香の模様 | Genji-kō no Moyō | Genji-kō Pattern | 400,000 |
| 源氏香模様 | Genji-kō Moyō | Genji-kō Design | 479,000 |
| 源氏香文様 | Genji-kō Monyō | Genji-kō Motif | 129,000 |
Appendix E: Asymptotic Behavior
The Bell numbers grow very fast. The asymptotic growth is approximately:
\[ B_n \sim \frac{1}{\sqrt{2 \pi n}} \left( \frac{n}{\ln n} \right)^n \]
Which is just a tiny bit slower than factorials, as you can see if you compare it to Stirling’s approximation.
Footnotes
† By "inside", I mean which respect to interval logic, not set containment. Obviously no group will be a subset of another, because no incense belongs to more than one group. But when the leftmost element of a group is to the left of the leftmost element of another, and likewise mutatis mutandis for the rightmost, then visually the second group is inside the first. Back
* I know I should cite the creators of these misguided images, but I have not done so to spare any potential embarrassment. You can find the originals through a Google reverse image search if you're curious. Back

