
A Seriously Slow Fibonacci Function
I recently wrote an article which was ostensibly about the Fibonacci series but was really about optimization techniques. I wanted to follow up on its (extremely moderate) success by going in the exact opposite direction: by writing a Fibonacci function which is as slow as possible.
This is not as easy as it sounds: any program can trivially be made slower, but this is boring. How can we make it slow in a fair and interesting way? The answer is to use a model of computation which is not deliberately designed to be slow but which in practice is quite slow, usually because the designer had something quite different than performance in mind.
While there are several to choose from, I selected the \(\lambda\)-calculus (read “lambda calculus”) as being particularly easy to write an spectacularly inefficient implementation in.
Some of you no doubt will be having flashbacks at the mention of the name, while others have already started slowly edging their mouse towards the close tab icon. But don’t worry - if you done any programming before you’ve already seen all the “hard” ideas associated with it and what’s left is a “toy” language that can be learned in a few minutes. By the end of this article you will see clearly how you could write your own non-trivial programs directly in the \(\lambda\)-calculus.
In fact, it’s main problem is that it’s too simple: it is difficult at first to see how anyone could do anything with it. Luckily for us, there exists a set of macros which turn the \(\lambda\)-calculus into a much higher level language. While Alonzo Church was inventing the \(\lambda\)-calculus itself he also developed this set of macros in parallel so that he could convince himself and others that it really could compute. These macros provide a simple and concrete way of encoding numbers, mathematical operators, boolean logic, and even data structures like lists, maps, and trees. Today, this technique is called Church encoding. If \(\lambda\)-calculus is machine code, then the Church encoding is C.
Goal
David Allen says to begin with the goal in mind, so let’s take a look at what we’re shooting for. As a blueprint, let’s first look at a performance-naive implementation of a function which finds the \(n\)-th Fibonacci number, implemented in vanilla Python:
def fibonacci(n):
if n <= 1:
return n
else:
return naive_fib(n-1) + naive_fib(n-2)Let’s put together a shopping list of features we need to implement this function:
- natural numbers
- addition
- subtraction
- less than comparison
- if/else branch
- recursion
Well, we certainly have our work cut out for us, don’t we? The first four require a model of the Peano axioms, the if/else branch requires a model of Boolean algebra, and recursion is usually regarded as a non-trivial language feature.
For the purposes of this article, we’re going to take a non-standard approach and not use the original notation. Instead, we’ll use a subset of Python which has a one-to-one correspondence with the \(\lambda\)-calculus but which is hopefully both more familiar and more accessible to readers: all of the code in this article will run in any Python 3 interpreter so that readers may follow along and try their own experiments if they like. I shall call this subset the “Pythonic” \(\lambda\)-calculus when I want to specifically refer to the lambda calculus implemented as a subset of the Python grammar.
In the next section I will describe this subset more formally. In this section, I’ll just do a quick high-level overview so you have some idea of where we are heading.
Basically, we’ll be writing Python code, but restricting ourselves to only
using the anonymous function syntax (e.g., lambda x: ...) and function calls
(e.g., f(x)).
In addition, we will expand our language with definitions, which are basically macros with a human readable name that expand out to \(\lambda\)-calculus expressions. Here is an example of a definition, the contents of which we will return to later:
plus = lambda m: lambda n: lambda f: lambda x: m(f)(n(f)(x))Definitions get substituted into other expressions very much like running “Find and Replace All”:
s/plus/(lambda m: lambda n: lambda f: lambda x: m(f)(n(f)(x)))/gBy introducing definitions, we will gradually build up a surprisingly high-level and expressive language on top of the \(\lambda\)-calculus. We can then revert to proper \(\lambda\)-calculus at any time by simply expanding out all the definitions like macros.
With those preliminaries out of the way, let me show you are goal. Although we will the rest of this article to understand in detail how it works, we will end up with a Fibonacci function that looks something like this:
fibonacci = Y(lambda f: PIR(
# define function f(n) as:
lambda n: (
# if n < 2
less_than(n)(two))
# then n
(n)
# else f(n-1) + f(n-2)
(plus
(f(minus(n)(one)))
(f(minus(n)(two))))))As always in Python, # indicates an non-executable comment.
It shouldn’t be to hard to see the basic shape of the familiar, friendly
Fibonacci function in there. If you have any LISP, it will even look vaguely
familiar, although the parentheses are in slightly different places. (In LISP,
function application looks like (minus n 2) instead of minus(n)(two).)
The Pythonic Lambda Calculus
In the \(\lambda\)-calculus there are only two operations: abstraction and application. These two can be composed to write any program (computable function) that has or ever will be written.
What do we mean by the term “abstraction?” Let’s say we have a concrete
calculation, such as the sums of squares of a vector like (3, 4). We could
type the following into a Python interpreter:
3*3 + 4*4In an interactive programming session, this might suffice: you type something
in and hit ENTER to see the answer. But in most cases values 3 and 4 are too
hard-coded to be useful. So we can abstract this by replacing 3 with a
placeholder variable x and introducing a function of x:
def half_ss(x):
return x*x + 4*4Now that we have an abstraction, a.k.a. a function, how do we use it? Before
we can do any concrete computation, we need to know what x is supposed to be.
This is called function application or simply application, and we use the
familiar f(x) syntax common to math and almost all programming languages.
half_ss(3)But this “half” function isn’t very satisfactory. The 4 is still hard coded.
If we want to do the same thing again and abstract 4 into y, we have a
couple of choices. We could greatly complicate our language and add another
syntactic primitive ,:
def half_ss(x, y):
return x*x + y*y
ss(3, 4)But if we want to keep things simple, why don’t we simply perform abstraction twice?
def ss(x):
def half_ss(y):
return x*x + y*y
return half_ssNote that when we call ss(3), what is returned is again a function, so
we can use a second application to pass the second argument:
ss(3)(4)The two applications “cancel out” the two abstractions, and we are left with
the concrete value 3*3 + 4*4, more commonly known as 25.
This works because we call ss with the first argument and instead of resolving
to a value, it instead returns a function that we can call with the second argument
to get the result. We can repeat this operation as many times as necessary, but
it get’s inconvenient to make up a silly name like half_ss each time; instead
we’ll use an anonymous lambda function:
ss = lambda x: lambda y: x*x + y*y
ss(3)(4)So to recap, we implement the abstraction operation of \(\lambda\)-calculus in
Python by using a lambda expressions with a single argument each, and if we
want to define a function that takes more than one argument we stack up lambda
expressions like lambda x: lambda y: lambda z :... .
Note that we can write our entire program without recourse to any names if
we treat ss as a definition and replace the string ss with its right-hand
side where ever it appears. The final program is:
(lambda x: lambda y: x*x + y*y)(3)(4)Which you can run and verify that it gives the answer 25.
In the \(\lambda\)-calculus, application is the only way we can do anything, so we should re-write the binary expressions as more primitive functions:
(lambda x: lambda y: plus(mult(x)(x))(mult(y)(y)))(3)(4)One specific trick deserves attention. We could define a constant function like so:
lambda x: cWhen called, this function ignores the argument x and always returns the
constant c. This expression however, has c as a free variable: there is
no lambda c: above it. We can remedy that with another abstraction:
lambda c: lambda x: cThis gives us a way to construct constant functions out of any value. This kind
of thing is called a closure. Closures have the property that they can
“remember” values assigned to them at runtime. In fact, the function ss
defined above also returned a closure, which “remembered” that x was supposed
to equal 3 until the time came when a concrete calculation could be carried
out. Closures are extremely important in the \(\lambda\)-calculus because they are
our only way of defining data structures and passing state around.
Setting aside closures, let’s next discuss how computation is actually carried out. You may well have noticed that the operation I’ve called “application” shows the syntax that says a function should be called with a certain argument, but I haven’t said anything about how the calling of a function should actually be carried out!
It turns out this is exactly the reverse of abstraction - we replace abstract
variables with concrete values. This is called the \(\beta\)-reduction rule (read
“beta reduction”.) For example, we may call the function lambda x: x(x)(x)
with concrete value t by writing (lambda x: x(x)(x))(t). The
\(\beta\)-reduction rules allows us to remove the lambda x and go through and
replace every x in the body of the function with t, which leaves us with
t(t)(t). Since t is a free variable, we cannot reduce this any further, so
we stop. Let’s do the same thing to our sums-of-squares example:
(lambda x: lambda y: plus(mult(x)(x))(mult(y)(y)))(3)(4)
(lambda y: plus(mult(3)(3))(mult(y)(y)))(4)
plus(mult(3)(3))(mult(4)(4))Since plus, mult, and even 3 and 4 are just definitions, we could
expand those definitions and continue the beta-reduction process until only a
single concrete value remains. Below, we will study the Church encoding for
natural numbers and learn exactly how to do this.
So abstraction introduces lambda expressions, application tells us when we should call a function and which argument to pass in, and \(\beta\)-reduction tells us how to carry out that function call.
There is one other rule, called \(\alpha\)-replacement (read “alpha replacement”), which tells us that we can change the variable names of functions whenever we want, as long as we are consistent and change it everywhere inside the body of the function too while also avoiding conflicts with other variable names. For example, these two lambda expressions are the same, and we can use the \(\alpha\)-replacement rule to transform one into the other and vice versa:
lambda x: x === lambda y: y
lambda x: x !== lambda x: yThe lambda expression lambda x: y on the other hand, would not be the same
because we cannot replace x with y without a conflict. We could change
lambda x: y into lambda z: y, but that would be a different function. This
rule should be intuitively obvious. It’s also not particularly important
because we equally well could have used an infinite sequence of variable
names to avoid conflicts; this would eliminate the need for the
\(\alpha\)-replacement rule. The \(\beta\)-reduction rule captures the very
essence of what it means to carry out a computation; the \(\alpha\)-replacement
rule is book-keeping.
The above gives the flavor of the \(\lambda\)-calculus: abstraction, application, \(\alpha\)-replacement and \(\beta\)-reduction. Since the \(\lambda\)-calculus is Turing complete, this can be interpreted as implying that all programming can be reduced to abstraction and application, and all computation can be reduced to the \(\beta\)-reduction rule; all else is vanity and grasping at wind.
But the examples I’ve used have share the weakness that if you go far enough
down, you are relying on other operations. For example, mult = lambda x: lambda y: x * y is ultimately defined in terms of the built-in multiplication
operation *, and x and y are are of type int. This won’t do; indeed,
this is a serious defect, because the whole point of the lambda calculus is to
prove that these two operations suffice to define any computable function.
Copping out halfway through and relying on native operations proves nothing.
To correct this defect, we need to start from scratch and scrupulously avoid
using any operation except for abstraction and application. Happily, Church
encoding provides a roadmap… it will however lead us to types and data
structures very different than the native python int and bool!
Formal Grammar
The subset of Python which constitutes the Pythonic \(\lambda\)-calculus can fully described by this BNF specification:
<expression> ::= <variable>
| "(" lambda <var> ":" <expression> ")"
| <expression> "(" <expression> ")"In plain english, we build up expressions recursively out of variables, lambda functions, and function applications.
In some cases, where it causes no ambiguity, we will omit the parentheses
around lambda functions, or add parentheses around function application e.g.
(f(x)). Note that the placement of parentheses is rather different than in
the original \(\lambda\)-calculus syntax! Where we might have written \((f x y)\) in
the convential notation we will write f(x)(y), and where we would have
written \((f (x y))\) we will write f(x(y)). Hopefully, the Pythonic notation
for function application will actually be more familiar to those of you who
have studied modern high level programming languages or pure mathematics.
As a convenience, we will also allow ourselves definitions, although we will later show that these definitions are merely a convenience and can be done away with whenever we choose through the simple process of string substitution. (The development of the Church encoding proceeds mainly by means of such definitions.) A definition looks like this:
<definition> ::= <definition-name> "=" <expression>Where the <expression> on the right is restrictions to have no free
variables. That is to say, every variable used is in fact inside the body of a
lambda function with that variable as a parameter. For example, lambda x: x(x)(x(x)) has no free variables, but lambda x: y(x) has y as a free
variable. Furthermore, while definitions can contain other definitions,
they cannot ever contain themselves, not even implicitly hidden away in
some other definition. Otherwise, the simple string substitution macro
expansion of a definition would never terminate! (Later, when we need recursion
to implement the Fibonacci function, we will need to find a way to do this!)
These restrictions exist so that we can think of our extended grammar as nothing more than a set of lightweight macros on top of the \(\lambda\)-calculus. In principle, for any given program written in the extended grammar, we can simply substitute in the body of the definition wherever we find the name of the definition. This takes only a finite number of steps and is guaranteed to terminate. At the end of this process, we are left with an equivalent program with no definitions or definition names. Furthermore, we can complete this “macro preprocessing” step entirely before beginning to run the program. In this sense, it is ancillary to the real calculation.
BTW, these rules for what constitutes a valid definition (as opposed to an axiom) can be traced back to Frege, who needed it because he was in the process of adding quantifiers over bound variables to logic. It turned out be a very fruitful principle; modern mathematics is 99% definitions, with only a handful of axioms holding up the foundation. It’s also very broad - even though the \(\lambda\)-calculus is not a logic, the concept of “definition” remains much the same.
To wrap up, the full extended grammar looks like this:
<definition> ::= <definition-name> "=" <expression>
<expression> ::= <variable>
| "(" lambda <var> ":" <expression> ")"
| <expression> "(" <expression> ")"
| "(" <definition-name> ")"Both the original grammar and the extended grammar are strict subsets of Python, and as such is runnable on a Python interpreter. This is, perhaps, the most extreme example of programming “into” a language instead of programming “in” a language, following McConnell’s distinction.
Note that if we run an expression in the extended grammar directly in Python, the interpreter does not do the macro expansions as described above… but the results of the calculations will always be identical if we’ve carefully followed the rules for introducing definitions! Later, we will show examples of running programs both ways.
Church Booleans
We’ll start with the simplest item on our shopping list: Boolean logic. There are only two Boolean values:
# Church Booleans
true = lambda x: lambda y: x
false = lambda x: lambda y: yNote that these are not the same as Python’s built-in True and False
constants; our lowercase true and false appear to Python as callable
objects of type function, not objects of type bool.
Some of you may object that these are not values, these are functions. Of course they are; the \(\lambda\)-calculus is made out of nothing but functions! But that doesn’t prevent us from thinking of some functions as values when it is convenient for us. Consider the “objects” of object-oriented programming - an object is nothing but a collection of functions, but we usually think of objects as values.
More generally, it is often convenient to talk about the “type” of different lambda expressions. However, because we are technically working in the “untyped” \(\lambda\)-calculus, we will have to keep the concept of “type” high-level and informal for now. (There are also “typed” versions but we don’t need it to actually compute stuff.)
Since we are keeping things informal, we can use an intuitive definition: the “type” of an expression is roughly the number and types of the parameter it would normally be called with. In high level languages this is often called the function signature. The two Church Booleans we defined both have the same type - they expect to be called with two arguments and will then return one or the other of those two arguments unchanged.
Consider the following function, which takes a Boolean argument:
lambda p: p(a)(b)This piece of code will work equally well if p is true or false - only
the behavior will be different. If p is true, it will return a and if p
if false it will return b. In other words, it has the same semantics
as an if/else statement or the ?: ternary operator.
In general, if we have a predicate (an expression which evaluates to a Boolean), we can always write an if/else statement like:
((<predicate>)
(<if-expression>)
(<else-expression>))While we will have to wait until after we’ve defined the Church numbers to
get really useful predicates like less_than, we can go ahead and define
the usual Boolean operators purely in terms of our above definitions for true
and false:
# Boolean logic
AND = lambda x: lambda y: x(y)(false)
OR = lambda x: lambda y: x(true)(y)
NOT = lambda x: x(false)(true)
XOR = lambda x: lambda y: x(NOT(y))(y)Each of these expects to be passed Boolean values and then returns a single
Boolean value. We can unpack these using the above equivalence to if/else;
for example, AND reads as “if x is true, then return y, else return false”.
This will return true only if x and y are both true, so this function
acts like “and”. You can read the other definitions in the same way.
To more easily interface with these functions, let’s write some bridge code:
from typing import Callable, Any
def church_to_bool(b: Callable) -> bool:
return b(True)(False)
def bool_to_church(b: bool) -> Callable:
return true if b else falseNow that we have these bridge functions, it’s fairly easy to write a test demonstrating that we’ve correctly implemented the truth tables for each of Boolean operation:
for x in (True, False):
for y in (True, False):
x_c = bool_to_church(x)
y_c = bool_to_church(y)
z_c = AND(x_c)(y_c)
z = church_to_bool(z_c)
print(x, "AND", y, "=", z)
True AND True = True
True AND False = False
False AND True = False
False AND False = False
At this point I encourage you to try to test some of the other Boolean
operators, and to write your own, such as NAND or the SUM and CARRY of a
full adder for more of a challenge.
This has been our first taste of computing the \(\lambda\)-calculus. The pattern (which we’ll soon see more of) is simple: use Church encoding to somehow translate your input values into lambda expressions. Pass those into a lambda expression which represent your program. Finally, reverse the Church encoding to recover meaningful values.
Church Numerals
The Church encoding of the natural numbers, called Church numerals, defines the
number \(n\) to be a binary function (here, “binary” means taking two arguments)
which takes a function f and an arbitrary value x and applies f to x
exactly \(n\) times:
zero = lambda f: lambda x: x
one = lambda f: lambda x: f(x)
two = lambda f: lambda x: f(f(x))
three = lambda f: lambda x: f(f(f(x)))
# ... and so onHow do you apply a function zero times? Well, you don’t; you just return the
value x right away. To call it once is f(x), twice is f(f(x)), and so on.
This means that Church numbers are not an arbitrary sequence of symbols
that only gain semantics because of the relations defined on them (as they are
in other models) but actually have behavior which is directly related to
their meaning: the \(n\)-th Church number has the behavior of repeating a
computation \(n\) times.
For example, suppose we have a function called greet and we want to call it 3
times. How would we implement the equivalent of a for or while loop in the
Pythonic lambda calculus? Just so:
def hello_world(n):
print(f"Iteration #{n}: Hello, Lambda Calculus!")
return n+1
three(hello_world)(1)
Iteration #1: Hello, Lambda Calculus!
Iteration #2: Hello, Lambda Calculus!
Iteration #3: Hello, Lambda Calculus!
4The first time greet() is called, it is called with the 1 we passed in. Each
subsequent call is passed the return value from the previous call. The function greet()
will be called 3 times in total, printing a message each time. Finally, it returns
a value of 4.
Of all the high-level programming languages I am aware of, I think only Ruby
comes close to the idea that numbers should literally be their own for
loops. Even LISP and Haskell require recursion, a separate map function,
or a loop macro. (For code readability alone this is probably a good
thing, though. In writing this article I’ve found the lack of traditional
signpost statements more confusing than elegant, and have had to use comments
to indicate where such control flow statements were being used.)
This one-to-one correspondence between Church numerals and behaviors makes it relatively easy to define mathematical operations on Church numerals. Following Peano, the first thing we need is a successor function which can increment a number by one:
succ = lambda n: lambda f: lambda x: f(n(f)(x))Why does this work? Well, given an original number n, it first uses n
to apply f to x \(n\) times. It then applies f once more itself. Thus,
the final value will be f applied to x \(n+1\) times, which is \(n+1\) by
definition.
This successor function allows us to easily construct new numbers ad infinitum:
# 0-10 for convenience
zero = lambda f: lambda x: x
one = lambda f: lambda x: f(x)
two = succ(one)
three = succ(two)
four = succ(three)
five = succ(four)
six = succ(five)
seven = succ(six)
eight = succ(seven)
nine = succ(eight)
ten = succ(nine)
church_digits = [zero, one, two, three, four, five, six, seven, eight, nine]We can now define other mathematical operators:
# church numerals
plus = lambda m: lambda n: lambda f: lambda x: m(f)(n(f)(x))
mult = lambda m: lambda n: lambda f: lambda x: m(n(f))(x)
exp = lambda m: lambda n: n(m)
pred = (lambda n:
lambda f: lambda x:
n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u))
minus = lambda m: lambda n: n(pred)(m)Of these, plus and mult are the easiest to understand. plus first applies
f to x \(m\) times, then applies f to the result \(n\) times, for a total of
\(n+m\) applications. The multiplication operator mult is similar, but does
things in a slightly different order: it first defines a new function g = n(f) which applies f to some value n times, and then applies g to x m
times. Since each call to g ends up calling f \(n\) times, the result is
that f is applied to x \(m \times n\) times.
Try to figure out exp for yourself. It’s equivalent to \(m^n\). It’s not on the
main line of functionality we need for the Fibonacci function, and it’s very
clever!
pred is the predecessor relation. It subtracts one from a number if possible.
(Zero is just mapped to zero, as negative numbers are not defined.) It’s
more complex than succ but studying it is extremely rewarding,
because it leads to understanding how data structures can be represented in the
\(\lambda\)-calculus. The basic idea is that we are going to but the value x in a
box and replace f with a different function, which I’ll call skip_first. The
first time skip_first is called, it sees that the box has not been opened, so
it opens that. After that, it sees that the box is already open, so it takes
the value out of the box, applies f to it once, and puts it back in the box.
It does this \(n\) times. At the end, it takes the value of the box. The
ultimate result is that f is applied to x \(n-1\) times, because nothing
happened the first time. In this analogy, the initial closed “box” is lambda u: x, the new box that is created after each step is lambda h: h(g(f)), and
the lambda u: u at the end is the final act of taking the value out of the
box.
pred is tricky understand, especially in this elementary form. The Wikipedia
article also has a pretty good explanation too. A good exercise to
manually work out the \(\beta\)-reduction of pred(two) to get a feel for it.
If it still gives you trouble, I suggest you leave it aside and study the rest
of theory until you learn how to encode the “pair” data structure. Then pred
much may be defined in a much more natural way. just to implement the
Fibonacci function so decided to take the straight path through the mud.
Nevertheless, there is a switchback trail with a very gentle slope right over
there.
Defining pred was the hard part. The definition of minus in terms of pred
is much easier: n applies the function pred to m \(n\) times, so we
subtract one \(n\) times, which is the same as subtracting n from m. Easy, yes?
Now that we have a reasonable set of mathematical operations, let’s do some practical examples. We can do basic operations like \(2+2\) or \(6 \times 7\):
plus(two)(two)
mult(six)(seven)The problem with these is that what they return is a Church numeral, which is a Python Callable. All I see on my screen when I run the above snippets is opaque and ambiguous output like this:
<function __main__.<lambda>.<locals>.<lambda>.<locals>.<lambda>(x)>To translate this back into something we can understand, we need to write another bridge function. But how can we “unpack” a Church number? Recall that the Church encoding of \(n\) is a function taking two arguments, a function \(f\) and a value \(x\), and it applies \(f\) to \(x\) \(n\) times: \(f^n(x)\). In our Python environment, this works even if \(x\) and \(f\) are not written in the lambda calculus. Therefore we can follow the spy pattern often used in unit testing and pass in an function which will report how often it was called.
def church_to_int(n: Callable) -> int:
return n(lambda x: x+1)(0)Going the other way requires no such tricks. If I want to encode the number 42 in the \(\lambda\)-calculus, I can use the first ten digits (defined above) and our mathematical operations to build up the Church number:
plus(mult(four)(ten))(two)We can use the same strategy for any number. All we really need to do is parse the base 10 representation of a number and build up the Church number in stages:
def int_to_church(n: int) -> Callable:
church_number = church_digits[ int(str(n)[0]) ]
for digit in str(n)[1:]:
church_digit = church_digits[int(digit)]
church_number = plus(mult(church_number)(ten))(church_digit)
return church_numberWe can now perform non-trivial calculations entirely in the \(\lambda\)-calculus:
> print("2 + 2 =", church_to_int(plus(two)(two)))
4
> print("6 * 7 =", church_to_int(mult(six)(seven)))
42Here is a much larger (and slower) example:
> a = int_to_church(1001)
> b = int_to_church(999)
> ab = mult(a)(b)
> print("1001 * 999 =", church_to_int(ab))
999999Now, finally, we can implement our sums-of-squares method:
> a = int_to_church(3)
> b = int_to_church(4)
> ss = plus(exp(a)(two))(exp(b)(two))
> print("3**2 + 4**2 =", church_to_int(ss))
25This isn’t all of number theory of course, but its enough to implement our little Fibonacci function!
Predicates Involving Numbers
The first and most basic predict test we need is a check for zero. This will form the foundation of all the other predicates:
is_zero = lambda n: n(lambda x: false)(true)This works because if lambda x: false is called even once, the result will be
false, and this can only be avoided if the function is never called, in which
case the original value true will be returned. But the only Church numeral
which never calls its function argument is zero, so the above function
returns true only for zero, and false for every other number.
By the way, a function which returns a value of type Church Boolean is the definition of a “predicate” in this context. The word carries no logical or semantic content here.
The fact that pred stops at zero (i.e., pred(zero) == zero) implies that
minus(x)(y) == zero if and only if y is bigger than or equal to x. We can
use this fact to define various comparison tests:
leq = lambda m: lambda n: is_zero(minus(m)(n))
less_than = lambda m: lambda n: leq(succ(m))(n)
eq = lambda m: lambda n: AND(leq(m)(n))(leq(n)(m))These functions are interesting because while the expect their arguments n
and m to be Church numbers, their return value is a Church Boolean. The main
thing we wanted was less_than, which we will need for our Fibonacci function.
Recursion
Rather than jumping straight into implementing recursion in the \(\lambda\)-calculus, let’s take it slow and develop the idea in stages. Let’s start with vanilla Python recursion:
def factorial(n):
if n <= 1:
return 1
else:
return n * factorial(n-1)This only works because by the time the interpreter reaches the statement
factorial(n-1) the global symbol table already contains an entry for
factorial, so Python happily resolves factorial to that function and calls
it. In other words, it works because Python is doing all the heavy lifting for
us!
In the \(\lambda\)-calculus, there is no global symbol table. Even if there were,
lambda functions are all anonymous: they don’t have names, so what would you
even query the symbol table for? The workaround is to pass the function into
itself as an argument. This is totally legal; x(x) is a perfectly cromulent
expression in Pythonic \(\lambda\)-calculus. Continuing with our factorial example a
little further, we have:
def _factorial(f, n):
if n <= 1:
return 1
else:
return n * f(f, n-1)
def factorial(n):
return _factorial(_factorial, n)
Neat. But it’s a little ugly that we have to make the recursive call as f(f, n-1)
and explicitly pass f back into itself. Why not make f a closure which Currys
that first argument for us?
def _factorial(f, n):
if n <= 1:
return 1
else:
return n * f(n-1)
def factorial(n):
f = lambda m: _factorial(f, m)
return f(n)We can make this more generic and reduce reliance on the global namespace by
passing _factorial in as an argument:
def call_recursively(f, n):
g = lambda m: f(g, m)
return g(n)
def _factorial(f, n):
if n <= 1:
return 1
else:
return n * f(n-1)
def factorial(n):
return call_recursively(_factorial, n)Finally, the call_recursively function can be abstracted entirely as a Python
decorator. (If you’re not familiar with the decorator syntax, @decorator/f is
simply syntactic sugar for f = decorator(f) and is a convenient way to apply
a functor to a function.)
def recursive(f):
def recursive(n):
g = lambda m: f(g, m)
return g(n)
return recursive
@recursive
def factorial(f, n):
if n <= 1:
return 1
else:
return n * f(n-1)
So, in vanilla Python, we’ve implemented a reusable utility which enables us to
conveniently do recursion while avoiding any reference to the global symbol
table. As we make the jump to the final form purely in Pythonic
\(\lambda\)-calculus, we will rename recursive to Y - it is indeed the famous
Y-combinator, the higher-order function which makes recursion (and therefore
also iteration) possible in the \(\lambda\)-calculus. As for why it is called
Y, I have no idea - it’s just the standard symbol.
Y = lambda f: (lambda x: x(x))(lambda y: f(lambda z: y(y)(z)))We can also apply exactly one application of the \(\beta\)-reduction rule to bring this into an equivalent symmetrical form:
Y = lambda f: (lambda y: f(lambda z: y(y)(z)))(lambda y: f(lambda z: y(y)(z)))While the symmetrical form is more often seen, I prefer the first version because I think it more clearly expresses the idea of currying a function with itself. However, both do exactly the same thing. Furthermore, neither have any free variables and so meet our requirements for a proper definition.
In an ideal world we could now define the recursive factorial function entirely in Pythonic \(\lambda\)-calculus like so:
factorial = Y(lambda f:
lambda n:
((leq)(n)(one)
(one)
(mult(n)(f(pred(n))))))However, there is a problem: when we run the above function we get a stack
overflow error. Why this so? Is the algorithm wrong? No: if you executed this
lambda expression with true \(\beta\)-reduction, it would work fine. The problem
is that our Church Boolean pseudo-if-else statement is not quite a proper
if-else! In a language like C or Python, the code inside the selected branch
will be executed, but code in the other branch will not even be run. However,
in the Pythonic \(\lambda\)-calculus, if we write:
((some-predicate)
(if-branch)
(else-branch))Then both the if-brach and the else-brach will need to be evaluated
completely before some-predicate can be called, regardless of the value of
some-predicate!
This is called “eager” evaluation and Python always eagerly evaluates all
arguments of a function call before performing the function call. Therefore
in Python, we will always compute both branches, and only at the very end
will we discard one of the values. Normally, this wouldn’t cause serious
problems because the answer would always be the same (it would just be a little
slower as it takes time to the work which gets thrown away.) It becomes a
serious problem in the case of recursion because the else branch is always
evaluated, which calls the function again, which calls the function again, and
so for forever.
One response would be to give up on Python and go abuse some other language which has lazy evaluation. (It’s not a coincidence that functional languages like Haskell generally support lazy evaluation!) Alternatively, we could write an interpreter for the \(\lambda\)-calculus which implements \(\beta\)-reduction rule, side-stepping Python entirely.
These are good options, and for someone writing a very complete implementation
of the \(\lambda\)-calculus they would be necessities. But today we’re only
concerned to write one function, the Fibonacci function, so we can use a much
simpler hack to prevent infinite recursion, which I will abbreviate PIR:
# cheap hack because true and false don't short circuit.
def PIR(f):
def wrapper_function(n):
if church_to_bool(is_zero(n)):
return zero
else:
return f(n)
return wrapper_functionWith our little hack in place, we can now implement a working version of the factorial function which does not cause a stack overflow:
factorial = Y(lambda f: PIR(
lambda n:
((leq)(n)(one)
(one)
(mult(n)(f(pred(n)))))))Long stacks of parentheses appear to be an operational hazard when working with \(\lambda\)-calculus inspired languages.
In any case, the above function is a little inconvenient to call because it requires a Church numeral as input and returns an opaque Church numeral. Let’s wrap it in bridge code:
def slow_factorial(n):
n = int_to_church(n)
fac = factorial(n)
return church_to_int(fac)This little function correctly computes factorials:
for n in range(1, 10):
print(n, slow_factorial(n))
1 1
2 2
3 6
4 24
5 120
6 720
7 5040
8 40320
9 362880
10 3628800What about our main design objective? I am pleased to report that the above function is indeedextremely slow: it takes over a minute to calculate \(10!\) on a fairly new laptop. That works out to 36 million times slower than the vanilla Python implementation.
We can profile the code to figure out why. Here, I’ve edited the profiler
output from %prun slow_factorial(9) to give names to the most common calls;
in the original the function name was always just (<lambda>) distinguished
only by line number.
ncalls tottime percall cumtime percall function
1564014 0.849 0.000 0.849 0.000 succ
362889 0.354 0.000 0.542 0.000 plus
362880 0.188 0.000 0.188 0.000 church_to_int
260669 0.152 0.000 0.152 0.000 zero
79211 0.052 0.000 0.052 0.000 pred
9/1 0.000 0.000 0.003 0.003 factorialSo, we actually spend almost all of our time simply incrementing numbers by one. Church numbers are easy to define and work with, but they are gloriously inefficient, especially as the numbers grow. A more efficient encoding could be defined by using the Boolean algebra we developed earlier to define operations on binary strings, but that is not what we are about today.
Final Fibonacci
Our shopping list is complete: we now have all the necessary tools to proceed to the endgame. All that remains is to implement the Fibonacci algorithm:
fibonacci = Y(lambda f: PIR(
lambda n:
less_than(n)(two)
(n)
(plus
(f(minus(n)(one)))
(f(minus(n)(two))))))The less_then(n)(two) is a predicate that resolves to a Church Boolean.
This Boolean is then used as an if/else statement returning n for the if
branch or the recurance relation for the Fibonacci for the else branch. The
else branch is simply the sum of \(F_{n-1}\) and \(F_{n-2}\). The Y-combinator
ensures that f is in fact the same fibonacci function so we can call
f(n-1) and f(n-2) to calculuate \(F_{n-1}\) and \(F_{n-2}\).
Because we make two separate recursive calls and don’t do any caching, the
number of calls to fibonacci() will grow roughly as \(\mathcal{O}(2^n)\). This
is of course a terrible algorithm; it’s the same one I called naive_fib() in
my earlier article on optimizing the Fibonacci function. However, this
is entirely in keeping with our goal of writing the slowest possible version!
As before, we’ll wrap this in bridge code to handle the translation between native Python integers and Church numerals:
def slow_fibonacci(n: int) -> int:
n = int_to_church(n)
fib = fibonacci(n)
return church_to_int(fib)We can test that it is correct by exhibiting the first 20 Fibonacci numbers:
for n in range(21):
print(n, slow_fibonacci(n))
0 0
1 1
2 1
3 2
4 3
5 5
6 8
7 13
8 21
9 34
10 55
11 89
12 144
13 233
14 377
15 610
16 987
17 1597
18 2584
19 4181
20 6765How Slow is Slow?
As expected, this is rather slow, over 6 seconds to calculate \(F_{20}\):
%time slow_fibonacci(20)
CPU times: user 6.59 s, sys: 20 ms, total: 6.61 s
Wall time: 6.6 sThis is one thousand times slower than the same naive algorithm in implemented vanilla Python, and about a million times slower than a good algorithm. Note however that this is still faster than a human could work it out on paper! As recently as 80 years ago this would have been state-of-the-art.
A straight line on a log-scale plot shows that the algorithm scales as \(\mathcal{O}(2^n)\).
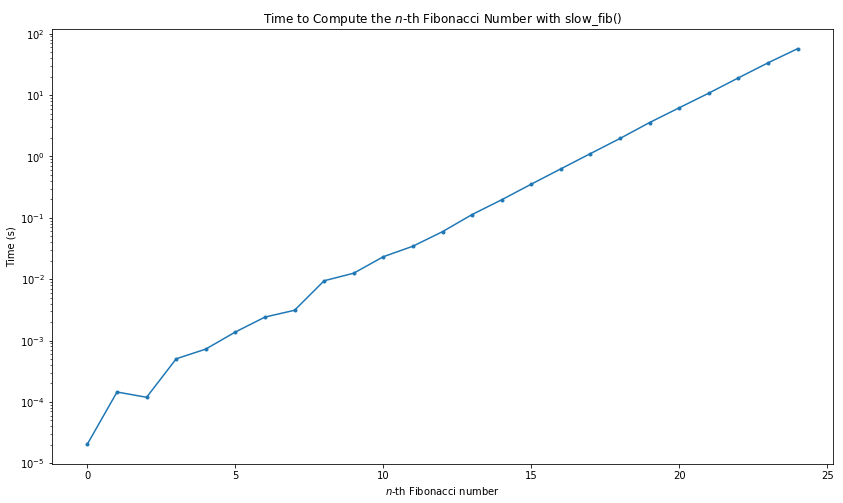
Timing Slow Fibonacci
The profiler shows where we were spending our time:
1922492 function calls (1833945 primitive calls) in 1.858 seconds
Ordered by: internal time
ncalls tottime percall cumtime percall function
1133885 0.513 0.000 0.513 0.000 pred
17710/1 0.199 0.000 31.615 31.615 fibonacci
95316 0.173 0.000 3.507 0.000 two
59896 0.159 0.000 3.636 0.000 mult
53131 0.118 0.000 30.497 0.001 is_zero
53130 0.110 0.000 0.280 0.000 minus
35421/1 0.092 0.000 31.615 31.615 PIR-wrapper
35420/2 0.083 0.000 31.615 15.807 Y
119792 0.074 0.000 0.074 0.000 three
35421 0.072 0.000 0.114 0.000 church_to_bool
17710 0.057 0.000 10.598 0.001 less_than
35420 0.052 0.000 0.076 0.000 fibonacci-wrapper
64077 0.041 0.000 0.041 0.000 zero
35420 0.024 0.000 0.024 0.000 PIR
17710 0.022 0.000 0.033 0.000 one
28655 0.014 0.000 0.014 0.000 false
24476 0.012 0.000 0.012 0.000 true
17710 0.012 0.000 0.012 0.000 leq
17711 0.012 0.000 0.012 0.000 plus
17710 0.012 0.000 0.012 0.000 succ
6765 0.006 0.000 0.006 0.000 church_to_intUnlike slow_factorial() which deals with numbers that blow up very
quickly, slow_factorial() deals with relatively smaller numbers which
means that we spent less time simply iterating through succ and more time
doing interesting things. Nevertheless, it spends a lot of time doing simple
subtractions - this is one of the weak points of the Church numerals.
Slower Than Slow
How could we make this even slower? Again, in a fair way, not just sprinkling no-ops and sleep statements throughout.
One interesting approach would be to implement what is sometimes called a meta-circular evaluator: an interpreter for the \(\lambda\)-calculus written entirely within the \(\lambda\)-calculus itself. We could then stack interpreters indefinitely, with each layer costing us another factor of a thousand. It would be reminiscent of this art project where a long gear chain is used to build a machine which will take 13.7 billion years for the final gear to complete one rotation:
The machine has a electric motor happily whirring away at one end (click the image for a video showing it action) and a solid block of concrete at the other. Normally that would be a recipe for disaster but because each gear steps the revolution speed down by a factor of 10, and because so many gears are chained together, the motion is infinitesimal by the end.
We’re not actually going to do that, of course. This article is already way too long. But we could.
Macro Expansion
Perhaps you don’t believe that this is really a \(\lambda\)-calculus program; after all, it has all those “definitions” which look suspiciously like named functions and in fact are being treated as named functions by the Python interpreter! Very suspicious.
We can see this is not the case by doing a search for each definition’s name
and replacing it with its body, and repeating until no named definitions are
left. Below is the step-by-step expansion process, with one version per line;
the last line contains no definitions (expect our PIR hack) and instead is
composed entirely of lambda functions, function calls, and bound variable
names.
fibonacci = Y(lambda f: PIR(lambda n: (less_than(m)(two))(n)(two)(n)(plus(f(minus(n)(one)))(f(minus(n)(two))))))
fibonacci = Y(lambda f: PIR(lambda n: (lambda m: lambda n: leq(succ(m))(n))(n)(two)(n)(plus(f(minus(n)(one)))(f(minus(n)(two))))))
fibonacci = Y(lambda f: PIR(lambda n: (lambda m: lambda n: (lambda m: lambda n: is_zero(minus(m)(n)))(succ(m))(n))(n)(two)(n)(plus(f(minus(n)(one)))(f(minus(n)(two))))))
fibonacci = Y(lambda f: PIR(lambda n: (lambda m: lambda n: (lambda m: lambda n: (lambda n: n(lambda x: false)(true))(minus(m)(n)))(succ(m))(n))(n)(two)(n)(plus(f(minus(n)(one)))(f(minus(n)(two))))))
fibonacci = Y(lambda f: PIR(lambda n: (lambda m: lambda n: (lambda m: lambda n: (lambda n: n(lambda x: (lambda x: lambda y: y))(lambda x: lambda y: x))(minus(m)(n)))(succ(m))(n))(n)(two)(n)(plus(f(minus(n)(one)))(f(minus(n)(two))))))
fibonacci = Y(lambda f: PIR(lambda n: (lambda m: lambda n: (lambda m: lambda n: (lambda n: n(lambda x: (lambda x: lambda y: y))(lambda x: lambda y: x))((lambda m: lambda n: n(pred)(m))(m)(n)))(succ(m))(n))(n)(two)(n)(plus(f((lambda m: lambda n: n(pred)(m))(n)(one)))(f((lambda m: lambda n: n(pred)(m))(n)(two))))))
fibonacci = Y(lambda f: PIR(lambda n: (lambda m: lambda n: (lambda m: lambda n: (lambda n: n(lambda x: (lambda x: lambda y: y))(lambda x: lambda y: x))((lambda m: lambda n: n(pred)(m))(m)(n)))(succ(m))(n))(n)(two)(n)(plus(f((lambda m: lambda n: n(pred)(m))(n)(one)))(f((lambda m: lambda n: n(pred)(m))(n)(two))))))
fibonacci = Y(lambda f: PIR(lambda n: (lambda m: lambda n: (lambda m: lambda n: (lambda n: n(lambda x: (lambda x: lambda y: y))(lambda x: lambda y: x))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(m)(n)))(succ(m))(n))(n)(two)(n)(plus(f((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(n)(one)))(f((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(n)(two))))))
fibonacci = Y(lambda f: PIR(lambda n: (lambda m: lambda n: (lambda m: lambda n: (lambda n: n(lambda x: (lambda x: lambda y: y))(lambda x: lambda y: x))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(m)(n)))(succ(m))(n))(n)(two)(n)((lambda m: lambda n: lambda f: lambda x: m(f)(n(f)(x)))(f((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(n)(one)))(f((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(n)(two))))))
fibonacci = Y(lambda f: PIR(lambda n: (lambda m: lambda n: (lambda m: lambda n: (lambda n: n(lambda x: (lambda x: lambda y: y))(lambda x: lambda y: x))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(m)(n)))(succ(m))(n))(n)(succ(one))(n)((lambda m: lambda n: lambda f: lambda x: m(f)(n(f)(x)))(f((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(n)(lambda f: lambda x: f(x))))(f((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(n)(succ(one)))))))
fibonacci = Y(lambda f: PIR(lambda n: (lambda m: lambda n: (lambda m: lambda n: (lambda n: n(lambda x: (lambda x: lambda y: y))(lambda x: lambda y: x))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(m)(n)))((lambda n: lambda f: lambda x: f(n(f)(x)))(m))(n))(n)((lambda n: lambda f: lambda x: f(n(f)(x)))(lambda f: lambda x: f(x)))(n)((lambda m: lambda n: lambda f: lambda x: m(f)(n(f)(x)))(f((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(n)(lambda f: lambda x: f(x))))(f((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(n)((lambda n: lambda f: lambda x: f(n(f)(x)))(lambda f: lambda x: f(x))))))))
fibonacci = (lambda f: (lambda x: x(x))(lambda y: f(lambda z: y(y)(z))))(lambda f: PIR(lambda n:(lambda m: lambda n: (lambda m: lambda n: (lambda n: n(lambda x: (lambda x: lambda y: y))(lambda x: lambda y: x))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(m)(n)))((lambda n: lambda f: lambda x: f(n(f)(x)))(m))(n))(n)((lambda n: lambda f: lambda x: f(n(f)(x)))(lambda f: lambda x: f(x)))(n)((lambda m: lambda n: lambda f: lambda x: m(f)(n(f)(x)))(f((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(n)(lambda f: lambda x: f(x))))(f((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda u: x)(lambda u: u)))(m))(n)((lambda n: lambda f: lambda x: f(n(f)(x)))(lambda f: lambda x: f(x))))))))The ultimate expanded version of this function works just as well and runs just as fast. Although it does nothing but create closures and call functions, somehow in the end it carries out the computation of a mathematical function. True, it is a little hard to read in this form, but so is machine code.
Here is a visualization of the full Fibonacci program (click for a larger image.) This shows every node (either a variable, function call, or lambda abstraction) as a binary tree.
It reminds me a lot of this XKCD comic strip about LISP where
cons is taken as atomic. Of course, the pair data structure
can easily be defined in the \(\lambda\)-calculus as well, making lambda
abstractions even more than fundamental cons. The essential insight remains
the same: all programs and data structures can be reduced to binary trees and
all information about the program is somehow contained in the very structure of
the tree itself.
Conclusion
All models of computation are equal, but some are more equal than others. In theory, the \(\lambda\)-calculus is only a constant factor away from any other model of computation, but the same is not true for the Church encoding: Church numerals are useful because they are very easy to “bootstrap;” that is to say, to implement in terms of lower level primitives, while on the other hand it is very difficult to implement more efficient numbers without data structures and a ready supply of distinct symbols, which the Church numerals provide.
It took us only a few dozen definitions to go from something so spartan that it seemed to be missing every convenience of modern programming, to a useful language with recursion, for loops, if/else statements, and recursive function calls. Things like closures, Currying, functors/decorators, which are considered advanced features in other languages, we somehow got for free.
If we had carried on defining signed numbers, pairs, lists, associative maps, and so on, this parsimony would continue and after a few hundred definitions - rather smaller than the standard library of most languages - we would have a perfectly functional language. (Pun absolutely intended.)
Some languages like Forth and io in fact take this exact approach:
the language is absolutely minimal and almost everything is moved to the
standard library, including the definition of standard constructs like for
and if/else.
If computation is so simple, why are modern languages so complicated? It mostly boils down to the impedance mismatch between the \(\lambda\)-calculus and the kinds of electronic computers we can actually build. We can’t actually make Church numerals fast, but we can make a machine which can perform mathematical operations on two 64 bit numbers in a single cycle. We can’t write a performant \(\beta\)-reducer, but we can write a block of machine code which calls functions by using a calling convention: pops a certain number arguments off the stack when called and returns a value on the stack or in a particular register. And so on.
For reasons that aren’t entirely clear to me, the \(\lambda\)-calculus has been a good model for thinking about high-level, expressive ways of computing, while the Turing machine has been a good model for designing actual computing machines. While in theory we can always switch from one model of computation to another, in practice this can involve a three or four order of magnitude reduction is performance. Practical programming languages have to walk the line between exposing the real capabilities of the machine while also providing useful high level abstractions.
Which isn’t to say there aren’t practical languages very much inspired by and very close to the \(\lambda\)-calculus. LISP and Haskell come to mind. After watching some of the SICP lectures on Youtube, I’m convinced the only reason Harold Abelson didn’t just teach the whole course in pure \(\lambda\)-calculus is because computers back then were still slow enough that it would have been just a little too painful, and LISP was chosen as a compromise. (Unfortunately, as we’ve seen today, this is still true. But maybe someday…) Many JavaScript programs too, particularly those that create lots of closures to handle asynchronous callbacks, seem to me to be much closer in spirit to the \(\lambda\)-calculus (as opposed to something like C, which uses a pointer machine model which is only slightly higher level than a Turing machine.) It’s never been more important to expose CS students to the idea and modes of thinking inspired by the \(\lambda\)-calculus and I think it’s importance will only grow as we can better afford the cost of abstractions.
As always, all the source code for this article is free and open source.
Postscript
Reading the “macro expanded version” of the function out loud, the similarity between “lambda” and “llama” made me think of the children’s book "Llama llama red pajama, a poem about a baby llama and his mama. I translated the above function declaration into a made up agglutinative language to produce this nonsense bedtime rhyme… perhaps the only one in the world which is also a executable program.
Hey llama baby hey llama mama hey
Ma sleep sleep hey llama ba baby
Hey llama ta ba hey ba sleep hey
Ta sleep sleep sleep sleep hey
Llama baby llama na hey llama ga
Llama na hey llama ga llama na
Hey llama na na hey llama ma hey
Llama ma llama ba ba sleep sleep
Hey llama ma llama ba ma sleep
Sleep hey hey llama ga llama na
Na hey hey llama na llama baby
Llama ma na hey llama red pajama
Llama haha hey red pajama hey
Baby sleep sleep sleep hey llama
Drama sleep hey llama dra dra
Sleep sleep sleep hey ga sleep
Sleep hey ga sleep hey na sleep
Sleep sleep hey hey llama na
Llama baby llama ma baby hey na
Hey baby sleep hey ma sleep sleep
Sleep hey ga sleep sleep hey na
Sleep sleep hey na sleep hey hey
Llama na llama baby llama ma baby
Hey na hey baby sleep hey ma
Sleep sleep sleep hey llama baby
Llama ma baby hey ma sleep sleep
Sleep hey na sleep hey hey llama
Ga llama na llama baby llama ma
Ga hey baby sleep hey na hey baby
Sleep hey ma sleep sleep sleep
Hey baby hey hey llama ga llama
Na na hey hey llama na llama baby
Llama ma na hey llama red pajama
Llama haha hey red pajama hey
Baby sleep sleep sleep hey llama
Drama sleep hey llama dra dra
Sleep sleep sleep hey ga sleep
Sleep hey na sleep hey llama baby
Llama ma baby hey ma sleep sleep
Sleep sleep hey baby hey hey
Llama ga llama na na hey hey
Llama na llama baby llama ma na
Hey llama red pajama llama haha
Hey red pajama hey baby sleep
Sleep sleep hey llama drama sleep
Hey llama dra dra sleep sleep
Sleep hey ga sleep sleep hey na
Sleep hey hey llama na llama baby
Llama ma baby hey na hey baby
Sleep hey ma sleep sleep sleep
Hey llama baby llama ma baby hey ma
Sleep sleep sleep sleep sleep sleep sleep


