The Prehistory of Computing, Part II

In part I of this two-part series we covered lookup tables and simple devices with at most a handful of moving parts. This time we’ll pick up in the 17th centuries, when computing devices started to became far more complex and the groundwork for later theoretical work began to be laid.

Pascal

We enter the era of mechanical calculators in 1642 when Pascal invented a machine, charmingly called the pascaline, which could perform addition and subtraction:

The Pascaline

The primary problem that must be solved to build a working adding machine, mechanical or electrical, is the carry. Yes, I’m talking about that operation you learned in elementary school, where you “carry the 1” when the digits in a column add up to more than 10. This problem is far less trivial than it sounds; even today, chip designers must decide to implement either a simple ripple-carry adder or one of many competing designs for a carry-lookahead adder depending on their transistor budget and logic depth. Carry, it turns out, is the very soul of the adding machine.

That’s why the pascaline represents such a crucial breakthrough: it featured the world’s first successful mechanical carry mechanism.

Still, the machine wasn’t very useful - adding and subtracting aren’t particularly hard, and the time spent fiddling with the dials to input the numbers easily dwarfed the time saved. The real prize would be a machine that could multiply and divide, and that was the problem that Gottfried Wilhelm von Leibniz set out to solve.

Leibniz

Leibniz, if you’ve only heard of him as a philosopher, may seem like an unlikely person to tackle this problem. In philosophy he’s chiefly remembered for his incomprehensible theory of monads and for stating that this was the best of all possible worlds, a point of view that was caricatured by Voltaire as the thoroughly unworldly and deeply impractical Dr. Pangloss in his novel Candide.

But of course he also helped invent Calculus, proved that kinetic energy was a conserved quantity distinct from momentum, designed hydraulic fountains and pumps, and generally produced an enormous body of work that was original, practical, and rigorous. If luminaries such as Voltaire viewed him as ridiculous, it was perhaps because he was too logical; or rather that he kept trying to apply rigorous logic to theology and the humanities, which is rarely a recipe for success.

In fact, Leibniz is something of an unacknowledged grandfather of computer science, with multiple parallel threads leading back to him. The first of these is mechanical computation. Leibniz built the first 4-operation calculator, which he called the stepped reckoner:

Leibniz's Stepped Reckoner

The name comes from a key internal component, the stepped drum, also known as the Leibniz wheel. This animation from Wikipedia perfectly illustrates its operation:

Each time the drum makes one complete revolution, the smaller red gear rotates by a number of ticks determined by its position. Slide the red gear to the top of the drum, and it will catch all nine teeth and advance a full revolution. Slide it part way down, and it will catch only some of the teeth and miss others, resulting in less rotation. Thus, if you slide the red gear to a position representing $n$ and perform $m$ complete rotations of the drum, the rotation of the red axle will encode $n \times m$. Furthermore, the carry increments by one each time the red axle completes one full rotation, so it’s not hard to imagine how a mechanical carry could be implemented. The full stepped reckoner is simply a series of Leibniz wheels coupled by the carry mechanism.

Leibniz worked on his machine for decades, producing a series of prototypes, giving live demonstrations, and writing several papers about it, but in his lifetime the machine never worked well enough to see any practical adoption. Despite its flaws, other inventors could see its potential and for the next two centuries, the Leibniz wheel and the Pinwheel calculator (a variation which also traces back to Leibniz’s 1685 book) would dominate the field. Nearly every mechanical calculator produced in this time derived from Leibniz’s ideas.

Two centuries later, the Leibniz wheel would form the basis of the first commercially successful mechanical calculator, the Colmar arithmometer. Even a cursory glance at its internals shows how little the basic design had changed:

So why did the Colmar succeed where Leibniz failed? The answer is simple: the vast improvement in precision machining techniques in the intervening centuries.

While we don’t have time to go into the full history of precision machining during the industrial revolution, suffice it to say that what was impossible for a lone craftsman in the 17th century was commonplace by the 19th. Leibniz himself lamented the difficulties, saying:

“If only a craftsman could execute the instrument as I had thought the model!”
—Leibniz

This is the main reason I don’t think we would have ended up with a steampunk computing era even if Leibniz or Babbage had gotten their machines to work—machines made of metal and gears are orders of magnitude slower, more expensive, and harder to work with than those made with CMOS and photolithography. (Matthew Jones goes into considerable detail about these technical and financial difficulties in his book, Reckoning with Matter.) While limited by the technology of his time, Leibniz clearly saw their vast potential:

“It is unworthy of excellent men to lose hours like slaves in the labour of calculation which could safely be relegated to anyone else if machines were used.”
—Leibniz

Formal Languages

There’s another thread that links Leibniz to modern computer science, on the theoretical rather than practical side. As a young man, he wrote a paper called On the Combinatorial Art where he envisioned encoding concepts as numbers and operating on them algebraically. Throughout the rest of his life, he tried to develop what he called “Characteristica universalis”, a kind of universal formal language. One of his attempts in this direction, the plus-minus calculus, was a formal, axiomatic language which presaged Boolean algebra and set theory. He dreamed of setting logic and mathematics on the same solid foundation as Euclidean geometry so that arguments could be formally verified:

“When there are disputes among persons, we can simply say, ‘Let us calculate,’ and without further ado, see who is right.”
—Leibniz

Leibniz’s ideas on this subject never got as far as he liked, but nevertheless proved fruitful—Frege cites Leibniz as an inspiration, placing him at the head of the chain that led to Russell, Gödel, and the entire field of formal logic and the foundations of mathematics. Today we have tools like Lean or Metamath which can automatically verify proofs.

When talking about Leibniz, it’s easy to forget he was working in the 17th century, not the 19th. His work would have been credible and relevant (and perhaps better appreciated) even two centuries later.

Approximation Theory

For this next section, I’m going to do something slightly inadvisable: I’m going to deviate from strict chronological order and jump ahead a few decades to discuss some mathematics that wasn’t fully developed until decades after Babbage’s career. Later, we’ll jump back in time to discuss the Difference Engine. This detour is necessary to appreciate why the Difference Engine (the sub-Turing precursor to the Analytical Engine) was such a good idea. Babbage certainly understood in a rough-and-ready way that finite difference methods were useful in approximating functions, but he couldn’t have known that in some sense they were all we really need, because Chebyshev hadn’t proved it yet.

Pafnuty Chebyshev was a 19th-century Russian mathematician who is best known for his theoretical work in number theory and statistics:

Chebyshev's Magnificent Beard

He was also very interested in the practical problem of designing linkages. A linkage is a series of rigid rods that sweep a particular motion. They are used in the design of everything from steam engines to oil pumps. Chebyshev even designed one himself that closely approximates linear motion over a portion of its path without undue strain on any of the rods:

Chebyshev Linkage

But it’s not linkages as such that we’re interested in, but rather how they inspired Chebyshev. Trying to design a linkage that approximates a certain path led him to the abstract mathematical question of how well we can approximate any function, which today we call approximation theory.

Chebyshev’s most important result in this area was the equioscillation theorem, which shows that any well-behaved continuous function can be approximated by a polynomial over a finite region with an uniform bound on error. Such approximations will “oscillate” around the true value of the function, sometimes shooting high, sometimes low, but always keeping to within some fixed $\varepsilon$ of the true value.

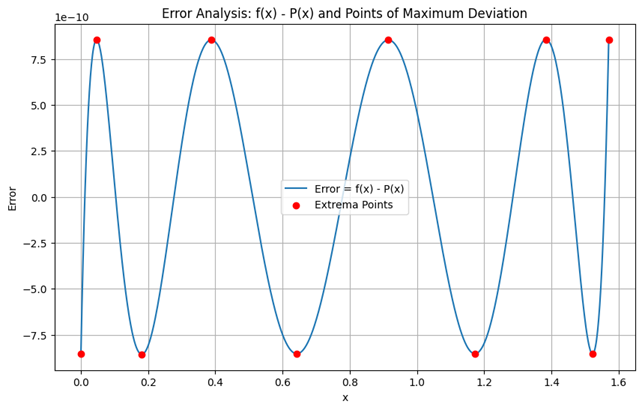
Equioscillation Example

Chebyshev’s proof was non-constructive—it didn’t tell you how to find such a polynomial, only that it exists—but it certainly waggled its eyebrows in that direction, and by 1934 Remez was able to work out the details of just such an algorithm. His algorithm tells us how to find the coefficients of a polynomial using only a hundred or so evaluations of the original function. It always works in theory and in practice it usually works very well. Note the scale of the y-axis on the above plot; it shows an 8th-degree polynomial approximating $\sin(x)$ to an absolute error of less than $10^{-9}$ over the region $[0, \tfrac{\pi}{2}]$. A 12th-degree polynomial can approximate it to less than the machine epsilon of a 64-bit float.

Its main practical limitation is that it requires the function to be bounded on the target interval, but for many functions such as $\tan(x)$ that have poles where it tends to infinity, the Padé approximant can be used instead. The Padé approximant is the ratio of two polynomials:

\[ R(x) = \frac{ \displaystyle \sum_{i=0}^m a_i x^i }{ \displaystyle 1 + \sum_{i=1}^n b_i x^i } = \frac{ a_0 + a_1 x + a_2 x^2 + \dots + a_m x^m }{ 1 + b_1 x + b_2 x^2 + \dots + b_n x^n } \]

This requires performing a single division operation at the end of the calculation, but the bulk of the work is simply evaluating the two polynomials.

It’s also true that the Remez algorithm only works over finite, bounded intervals, but that is easily remedied through the simple expedient of breaking the function up into different regions and fitting a separate polynomial to each.

The practical upshot of all this is that to this day, whenever you use a function from a standard math library when programming, it almost always uses piecewise polynomial approximation under the hood. The coefficients used for those polynomials are often found with the Remez algorithm since the uniform bound to error it offers is very attractive in numerical analysis but as they say on the BBC, other algorithms are available.

All of which is just a very long-winded way of saying polynomials are pretty much all you need for a huge subset of practical computing. So wouldn’t it be nice if we had a machine that was really, really good at evaluating polynomials?

The Difference Engine

Babbage’s first idea, the Difference Engine, was a machine for evaluating series and polynomials. If it had been built, it could have rapidly generated tables for 7th-degree polynomials to a high degree of precision and reliability.

“Just polynomials,” you might ask, “not trigonometric functions, logarithms, or special functions? Seems less useful than the older stuff we’ve already talked about.” Well, technically he proposed using the finite difference method, which is an early form of polynomial interpolation. This would have worked well, as we saw above.

OK, so how did Babbage propose to automate polynomial evaluation? The key idea is that differences turn polynomial evaluation into simple addition. If you have a polynomial $p(x)$ and you want its values at equally spaced points $x, x+1, x+2, \dots$, you can avoid recomputing the full polynomial each time. Instead, you build a difference table:

Once you know the starting value $p(x)$ and all the differences at that point, you can get every subsequent value just by repeated additions. Let’s take the following polynomial as an example:

\[ p(x) = x^3 - 2x^2 + 3x - 1 \]

If we first evaluate this polynomial at a number of evenly spaced points and then (working left to right) take the difference of consecutive rows, and take the differences of those differences and so on, we can construct a table like so:

$x$ $p(x)$ $\Delta p$ $\Delta^2 p$ $\Delta^3 p$
0 -1 2 2 6
1 1 4 8 6
2 5 12 14 6
3 17 26 20 6
4 43 46 26 6

Crucially, after three differences (the same as the order of our polynomial) the difference becomes constant. Why does that matter? Because we can reverse the process. Working right to left, we can compute the differences and ultimately $p(x)$ from the preceding row using nothing more complex than addition! Here we’ve taken an integer step for the sake of clarity, but this $\Delta x$ can be arbitrarily small, and the whole process can be used to create large tables with high precision. The Difference Engine would have automated this process, allowing it to generate large tables very efficiently.

The Difference Engine may not have had that magical Turing-completeness, but it was still a very clever and important idea.

Conclusion

You know the rest of the story. Babbage moved on from the Difference Engine to the much more ambitious Analytical Engine. Neither was successfully completed: as Leibniz had found centuries earlier, designing mechanical computers is a lot easier than actually getting them to work. Despite this, Ada Lovelace wrote the first computer program for it, targeting its envisioned instruction set architecture.

After Babbage, there was a brief era of electro-mechanical computers: Herman Hollerith and the punch card, the IBM 602 Calculating Punch, the delightfully named Bessy the Bessel engine, the Z3, and similar machines. Slide rules were still in common use until WWII, and mechanical calculators such as the Curta were still being manufactured as late as the 1970s. Meanwhile, Turing, Shannon, Church, Gödel, von Neumann, and many others were putting computer science on a firm theoretical foundation.

With the advent of the transistor, CMOS and photolithography, it was clear that digital was the way to go. Today, electronic computers are a billion (and, in some special cases like GPUs, a trillion) times faster than their mechanical counterparts, while also being cheaper and more reliable.

Despite this, not much has changed: we still use lookup tables, polynomial approximation, and logarithms as needed to speed up calculations; the only difference is we’ve pushed these down into libraries where we hardly ever have to think about them. This is undoubtedly a good thing:

“Civilization advances by extending the number of important operations which we can perform without thinking of them.”
—Alfred North Whitehead

But if we stand on the shoulders of giants today, it is only because generations of humans sat by smoky campfires scratching lessons onto bones to teach their children how to count beyond their number of fingers, or stayed up late into the night to measure the exact positions of stars, or tried to teach a box of rods and wheels how to multiply.

Archimedes once said, “Give me a place to stand and a lever long enough, and I will move the Earth.” It occurs to me that the computer is an awfully long lever, except what it multiplies is not mechanical force, but thought itself. I wonder what we will move with it.

Here are a few of the books I consulted while working on this article and which you may find interesting if you’d like to learn more about these topics:

Reckoning With Matter The Daring Invention of Logarithm Tables The Notebook: A History of Thinking on Paper A Little History of Mathematics

Note: I am not an Amazon affiliate, and I do not earn any commission from the links above.

Appendix B: IA and the Extended Mind Hypothesis

Implicit in the above is the idea that external devices, even those as simple as a clay tablet or a hinge, can be used to overcome our inherent limitations and augment our intelligence. This is sometimes called Intelligence Amplification (IA) in deliberate contrast to AI.

Here are a few of the seminal works in the genre:

Note that none of these require anything as invasive as a brain-computer interface but instead explore the implications of systems comprised of both a human and a computer.

While all these works are basically futurist in character, the concept also provides a very useful lens when looking back on the early history of computing.